Advertisements
Advertisements
प्रश्न
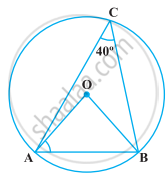
If O is the centre of the circle, find the value of x in the following figure
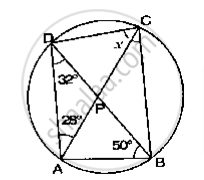
उत्तर
In ΔDAB by angle sum property
∠ADB + ∠DAB + ∠ABD = 180°
⇒ 32° + ∠DAB + 50° = 180°
⇒ ∠DAB = 180° - 32° - 50° = 98°
Now,
∠CAB + ∠DAB = 180° ...(Opposite angles of cyclic quadrilateral)
⇒ 98° + x = 180°
⇒ x = 180° - 98° = 82°
APPEARS IN
संबंधित प्रश्न
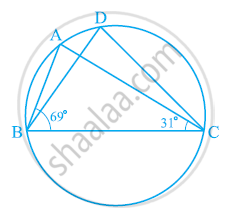
In the given figure, ∠ABC = 69°, ∠ACB = 31°, find ∠BDC.
Prove that the line joining the mid-point of a chord to the centre of the circle passes through the mid-point of the corresponding minor arc.
If O is the centre of the circle, find the value of x in the following figure
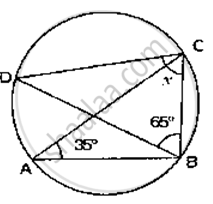
If O is the centre of the circle, find the value of x in the following figures.
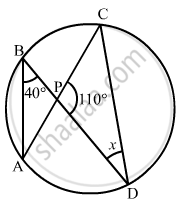
In the given figure, O and O' are centres of two circles intersecting at B and C. ACD is a straight line, find x.
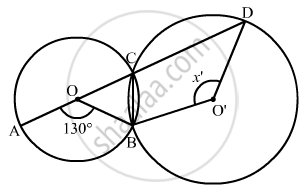
In the given figure, O is the centre of the circle, prove that ∠x = ∠y + ∠z.
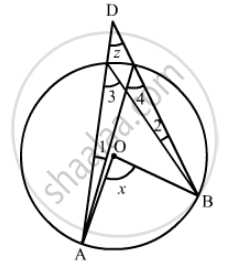
In the given figure, O is the centre of a circle and PQ is a diameter. If ∠ROS = 40°, find ∠RTS.
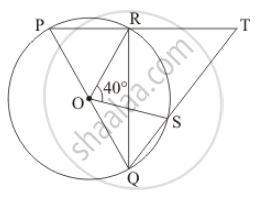
Prove that the angle in a segment shorter than a semicircle is greater than a right angle.
In the given figure, if ∠AOB = 80° and ∠ABC = 30°, then find ∠CAO.

In the following figure, ∠ACB = 40º. Find ∠OAB.