Advertisements
Advertisements
प्रश्न
If O is the centre of the circle, find the value of x in the following figure
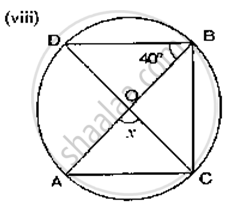
उत्तर
In DDAB, by angle sum property
∠ADB + ∠DAB + ∠ABD = 180°
⇒ 32° + ∠DAB + 50° = 180°
⇒ ∠OAB = 180° - 32° - 50°
⇒ ∠DAB = 95°
Now,
∠OAB + ∠DCB = 180°
∠ 98 + x = 180°
⇒ x = 180 - 98° = 82°
APPEARS IN
संबंधित प्रश्न
Fill in the blank:
Segment of a circle is the region between an arc and .................. of the circle.
Prove that a diameter of a circle which bisects a chord of the circle also bisects the angle subtended by the chord at the centre of the circle.
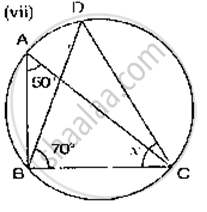
If O is the centre of the circle, find the value of x in the following figure:

If O is the centre of the circle, find the value of x in the following figure

If O is the centre of the circle, find the value of x in the following figure
In the given figure, it is given that O is the centre of the circle and ∠AOC = 150°. Find ∠ABC.

Prove that the angle in a segment shorter than a semicircle is greater than a right angle.
Prove that the line segment joining the mid-point of the hypotenuse of a right triangle to its opposite vertex is half the hypotenuse.
In the given figure, two congruent circles with centres O and O' intersect at A and B. If ∠AOB = 50°, then find ∠APB.

A circle has radius `sqrt(2)` cm. It is divided into two segments by a chord of length 2 cm. Prove that the angle subtended by the chord at a point in major segment is 45°.
