Advertisements
Advertisements
Question
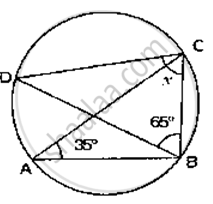
If O is the centre of the circle, find the value of x in the following figure
Solution
In DDAB, by angle sum property
∠ADB + ∠DAB + ∠ABD = 180°
⇒ 32° + ∠DAB + 50° = 180°
⇒ ∠OAB = 180° - 32° - 50°
⇒ ∠DAB = 95°
Now,
∠OAB + ∠DCB = 180°
∠ 98 + x = 180°
⇒ x = 180 - 98° = 82°
APPEARS IN
RELATED QUESTIONS
Prove that a diameter of a circle which bisects a chord of the circle also bisects the angle subtended by the chord at the centre of the circle.
Given an arc of a circle, show how to complete the circle.
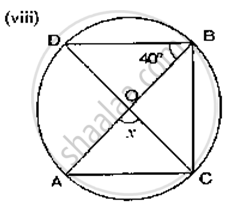
If O is the centre of the circle, find the value of x in the following figure:
If O is the centre of the circle, find the value of x in the following figure

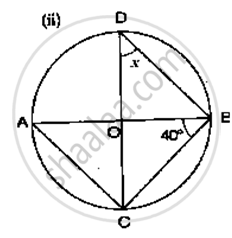
If O is the centre of the circle, find the value of x in the following figure

If O is the centre of the circle, find the value of x in the following figure
If O is the centre of the circle, find the value of x in the following figures.
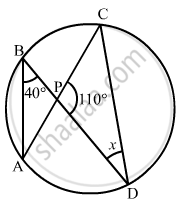
If O is the centre of the circle, find the value of x in the following figures.

In the given figure, O and O' are centres of two circles intersecting at B and C. ACD is a straight line, find x.
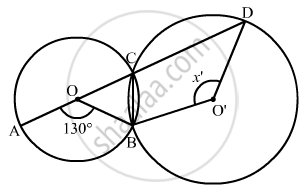
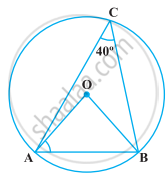
In the following figure, ∠ACB = 40º. Find ∠OAB.