Advertisements
Advertisements
Question
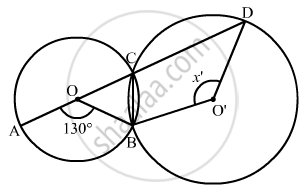
In the given figure, O and O' are centres of two circles intersecting at B and C. ACD is a straight line, find x.
Solution
It is given that
Two circles having center O and O' and ∠AOB = 130°
And AC is diameter of circle having center O
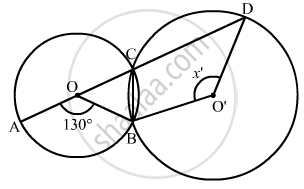
We have
`angle ACB =1/2 angleAOB = 65°`
So
`angleDCB = 180° - angleACB`
= 180° - 65°
= 115°
Now, reflex `angleBO'D = 2 angleBCD`
So
`360° - x° = 2 xx 115 `
= 230°
APPEARS IN
RELATED QUESTIONS
Fill in the blank:
A circle divides the plane, on which it lies, in ............ parts.
Given an arc of a circle, complete the circle.
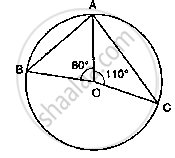
In the below fig. O is the centre of the circle. Find ∠BAC.
If O is the centre of the circle, find the value of x in the following figure:

If O is the centre of the circle, find the value of x in the following figure:
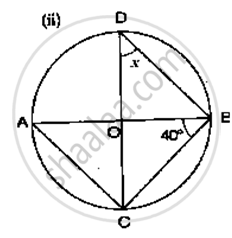
If O is the centre of the circle, find the value of x in the following figures.
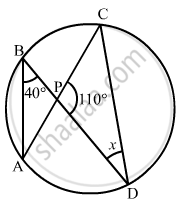
In the given figure, O is the centre of the circle, prove that ∠x = ∠y + ∠z.
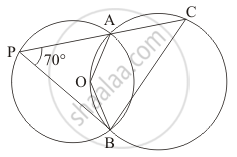
In the given figure, two circles intersect at A and B. The centre of the smaller circle is Oand it lies on the circumference of the larger circle. If ∠APB = 70°, find ∠ACB.
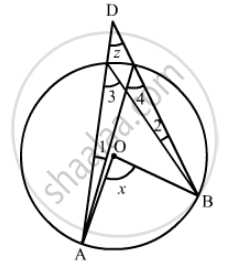
In the given figure, two congruent circles with centres O and O' intersect at A and B. If ∠AOB = 50°, then find ∠APB.

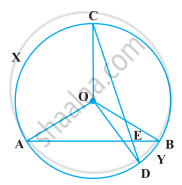
In the following figure, AB and CD are two chords of a circle intersecting each other at point E. Prove that ∠AEC = `1/2` (Angle subtended by arc CXA at centre + angle subtended by arc DYB at the centre).