Advertisements
Advertisements
Question
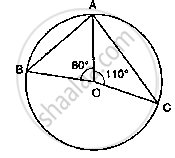
In the below fig. O is the centre of the circle. Find ∠BAC.
Solution
WE have `/_AOB=80°`
and ∠AOC =110°
∴∠AOB+∠AOC+∠BOC=360°
⇒80°+110°+∠BOC=360°
⇒∠BOC=360°-80°-110°
⇒∠B0C=170°
By degree measure theorem
∠BOC=2∠BAC
⇒170°=2∠BAC
⇒∠BAC=`(170°)/2=85°`
APPEARS IN
RELATED QUESTIONS
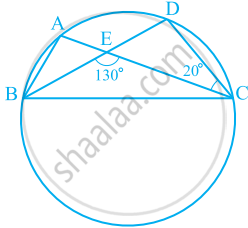
In the given figure, A, B, C and D are four points on a circle. AC and BD intersect at a point E such that ∠BEC = 130° and ∠ECD = 20°. Find ∠BAC.
If O is the centre of the circle, find the value of x in the following figure
If O is the centre of the circle, find the value of x in the following figure
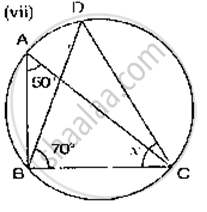
If O is the centre of the circle, find the value of x in the following figures.
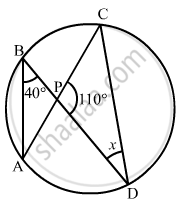
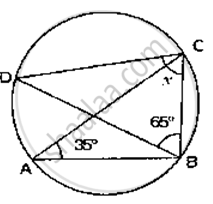
If O is the centre of the circle, find the value of x in the following figures.

O is the circumcentre of the triangle ABC and OD is perpendicular on BC. Prove that ∠BOD = ∠A
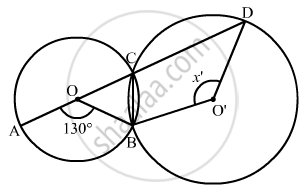
In the given figure, O and O' are centres of two circles intersecting at B and C. ACD is a straight line, find x.
In the given figure, if O is the circumcentre of ∠ABC, then find the value of ∠OBC + ∠BAC.

A chord of a circle is equal to its radius. Find the angle subtended by this chord at a point in major segment.
A circle has radius `sqrt(2)` cm. It is divided into two segments by a chord of length 2 cm. Prove that the angle subtended by the chord at a point in major segment is 45°.
