Advertisements
Advertisements
Question
A chord of a circle is equal to its radius. Find the angle subtended by this chord at a point in major segment.
Solution
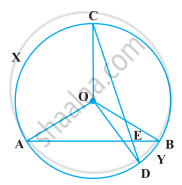
Given, AB is a chord of a circle, which is equal to the radius of the circle,
i.e., AB = BO ...(i)
Join OA, AC and BC.
Since, OA = OB = Radius of circle
OA = AS = BO
Thus, ΔOAB is an equilateral triangle.
⇒ ∠AOB = 60° ...[Each angle of an equilateral triangle is 60°]
By using the theorem, in a circle, the angle subtended by an arc at the centre is twice the angle subtended by it at the remaining part of the circle.
i.e., ∠AOB = 2∠ACB
⇒ ∠ACB =
APPEARS IN
RELATED QUESTIONS
Prove that the line joining the mid-point of a chord to the centre of the circle passes through the mid-point of the corresponding minor arc.
Prove that a diameter of a circle which bisects a chord of the circle also bisects the angle subtended by the chord at the centre of the circle.
Given an arc of a circle, show how to complete the circle.
If O is the centre of the circle, find the value of x in the following figure
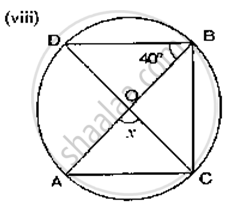
If O is the centre of the circle, find the value of x in the following figure
In the given figure, O and O' are centres of two circles intersecting at B and C. ACD is a straight line, find x.
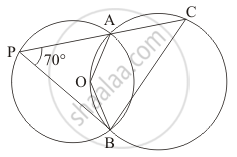
In the given figure, two circles intersect at A and B. The centre of the smaller circle is Oand it lies on the circumference of the larger circle. If ∠APB = 70°, find ∠ACB.
In the given figure, if ∠AOB = 80° and ∠ABC = 30°, then find ∠CAO.

In the given figure, if O is the circumcentre of ∠ABC, then find the value of ∠OBC + ∠BAC.

In the following figure, AB and CD are two chords of a circle intersecting each other at point E. Prove that ∠AEC =