Advertisements
Advertisements
Question
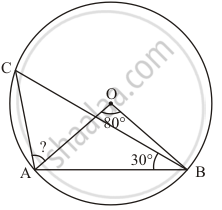
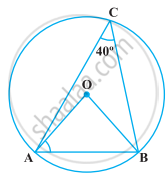
In the given figure, if ∠AOB = 80° and ∠ABC = 30°, then find ∠CAO.

Solution
Consider the given circle with the centre ‘O’. Let the radius of this circle be ‘r’. ‘AB’ forms a chord and it subtends an angle of 80° with its centre, that is`angleAOB ` = 80°.
The angle subtended by an arc at the centre of the circle is double the angle subtended by the arc in the remaining part of the circle.
So, here we have
`angleACB = ( angleAOB )/2`
`=(80°)/2`
`angleACB = 40°`
In any triangle the sum of the interior angles need to be equal to 180°.
Consider the triangle ΔAOB
`angleAOB + angleOAB + angleOBA = 180°`
Since, `OA = OB = r , we have `angle OAB = angleOBA `. So the above equation now changes to
`angleAOB + angleOAB + angleOAB ` = 180°
`2 angle OAB = 180° - angleAOB `
= 180° - 80°
`2angleOAB` = 100°
`angleOAB ` = 50 °
Considering the triangle ΔABC now,
`angleACB + angleOAB + angle OAC + angleABC ` = 180°
`angle OAC = 180° - angleACB - angleOAB - angleABC`
= 180°- 40°- 50° - 30°
`angleOAC` = 60°
Hence, the measure of `angleCAO ` is 60° .
APPEARS IN
RELATED QUESTIONS
Fill in the blank:
A circle divides the plane, on which it lies, in ............ parts.
If O is the centre of the circle, find the value of x in the following figure

If O is the centre of the circle, find the value of x in the following figure
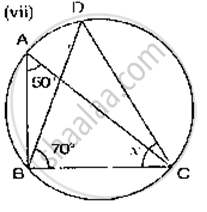
If O is the centre of the circle, find the value of x in the following figure
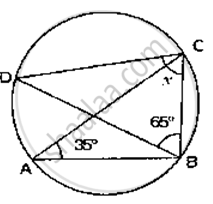
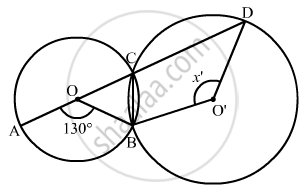
In the given figure, O and O' are centres of two circles intersecting at B and C. ACD is a straight line, find x.
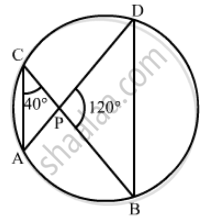
In the given figure, if ∠ACB = 40°, ∠DPB = 120°, find ∠CBD.
In the given figure, AB is a diameter of the circle such that ∠A = 35° and ∠Q = 25°, find ∠PBR.

If the given figure, AOC is a diameter of the circle and arc AXB = \[\frac{1}{2}\] arc BYC. Find ∠BOC.
In the following figure, ∠ACB = 40º. Find ∠OAB.
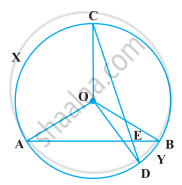
In the following figure, AB and CD are two chords of a circle intersecting each other at point E. Prove that ∠AEC = `1/2` (Angle subtended by arc CXA at centre + angle subtended by arc DYB at the centre).