Advertisements
Advertisements
Question
In the given figure, AB is a diameter of the circle such that ∠A = 35° and ∠Q = 25°, find ∠PBR.

Solution
Let us first consider the triangle ΔABQ.
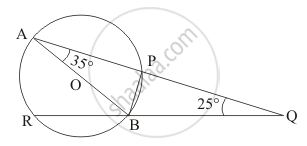
It is known that in a triangle the sum of all the interior angles add up to 180°.
So here in our triangle ΔABQ we have,
`angleBAQ + angleAQB + angleABQ ` = 180°
`angleABQ = 180° - angleBAQ - angle AQB`
= 180° - 35° - 25°
`angle ABQ` = 120°
By a property of the circle we know that an angle formed in a semi-circle will be 90°..
In the given circle since ‘AB’ is the diameter of the circle the angle `angleAPB` which is formed in a semi-circle will have to be 90°.
So, we have `angleAPB` = 90°
Now considering the triangle ΔAPB we have,
`angleAPB + angleBAP + angleABP ` = 180°
`angleABP = 180° - angleAPB - angleBAP`
= 180° - 90° - 35 °
`angleABP` = 55°
From the given figure it can be seen that,
`angleABP + anglePBQ = angle ABQ`
`anglePBQ = angleABQ - angleABP`
= 120°- 55°
`anglePBQ` = 65°
Now, we can also say that,
`anglePBQ + anglePBR` = 180°
`anglePBR = 180° - anglePBQ`
=180° - 65 °
`anglePBR ` = 115°
Hence the measure of the angle `anglePBR` is 115°.
APPEARS IN
RELATED QUESTIONS
In the below fig. O is the centre of the circle. Find ∠BAC.
If O is the centre of the circle, find the value of x in the following figure:

If O is the centre of the circle, find the value of x in the following figure:
If O is the centre of the circle, find the value of x in the following figure
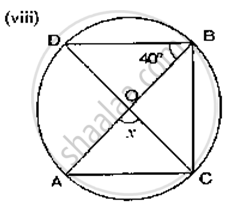
If O is the centre of the circle, find the value of x in the following figure
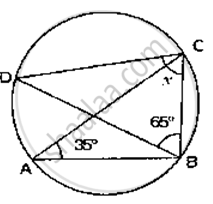
In the given figure, it is given that O is the centre of the circle and ∠AOC = 150°. Find ∠ABC.

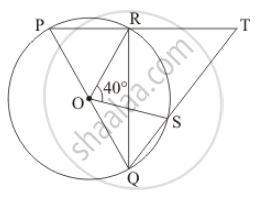
In the given figure, O is the centre of a circle and PQ is a diameter. If ∠ROS = 40°, find ∠RTS.
Prove that the angle in a segment shorter than a semicircle is greater than a right angle.
In the given figure, if ∠AOB = 80° and ∠ABC = 30°, then find ∠CAO.

If the given figure, AOC is a diameter of the circle and arc AXB = \[\frac{1}{2}\] arc BYC. Find ∠BOC.