Advertisements
Advertisements
Question
Prove that the angle in a segment shorter than a semicircle is greater than a right angle.
Solution
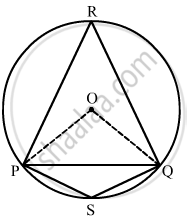
\[ \stackrel\frown{QP} \text{ is a major arc and } \angle PSQ \text{ is the angle formed by it in the alternate segment } . \]
\[ \text{ We know that the angle subtended by an arc at the centre is twice the angle subtended by it at any point of the alternate segment of the circle } . \]
`=> 2angle "PSQ" = "m"`
`=> 2angle "PSQ" = 360^circ - "m"`
`=> 2 angle"PSQ" = 360^circ - 180^circ ...(because angle "POQ" < 108^circ)`
`=> 2angle "PSQ" > 180^circ`
`=> angle "PSQ" > 90^circ`
Thus, the angle in a segment shorter than a semi-circle is greater than a right angle.
APPEARS IN
RELATED QUESTIONS
Prove that a diameter of a circle which bisects a chord of the circle also bisects the angle subtended by the chord at the centre of the circle.
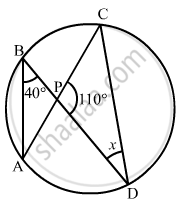
If O is the centre of the circle, find the value of x in the following figure
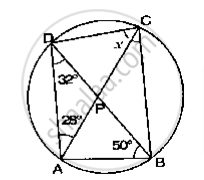
If O is the centre of the circle, find the value of x in the following figures.
In the given figure, it is given that O is the centre of the circle and ∠AOC = 150°. Find ∠ABC.

In the given figure, two congruent circles with centres O and O' intersect at A and B. If ∠AOB = 50°, then find ∠APB.

In the given figure, AB is a diameter of the circle such that ∠A = 35° and ∠Q = 25°, find ∠PBR.

In the given figure, P and Q are centres of two circles intersecting at B and C. ACD is a straight line. Then, ∠BQD =
In the given figure, if O is the circumcentre of ∠ABC, then find the value of ∠OBC + ∠BAC.

If ABC is an arc of a circle and ∠ABC = 135°, then the ratio of arc \[\stackrel\frown{ABC}\] to the circumference is ______.
The chord of a circle is equal to its radius. The angle subtended by this chord at the minor arc of the circle is
