Advertisements
Advertisements
Question
The chord of a circle is equal to its radius. The angle subtended by this chord at the minor arc of the circle is
Options
60°
75°
120°
150°
Solution
150°
We are given that the chord is equal to its radius.
We have to find the angle subtended by this chord at the minor arc.
We have the corresponding figure as follows:
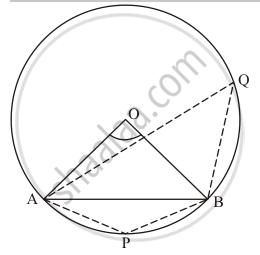
We are given that
AO = OB = AB
So ,
\[\bigtriangleup\] AOB is an equilateral triangle.
Therefore, we have
∠AOB = 60°
Since, the angle subtended by any chord at the centre is twice of the angle subtended at any point on the circle.
So `angleAQB =(angleAOB)/2`
`= 60/2 = 30°`
Take a point P on the minor arc.
Since `square APBQ` is a cyclic quadrilateral
So, opposite angles are supplementary. That is
`angle APB + angleAQB = 180°`
`angle APB + 30° = 180°`
`angleAPB = 180° - 30°`
`= 150°`
APPEARS IN
RELATED QUESTIONS
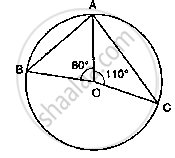
In the below fig. O is the centre of the circle. Find ∠BAC.
If O is the centre of the circle, find the value of x in the following figure:

If O is the centre of the circle, find the value of x in the following figure

O is the circumcentre of the triangle ABC and OD is perpendicular on BC. Prove that ∠BOD = ∠A
In the given figure, it is given that O is the centre of the circle and ∠AOC = 150°. Find ∠ABC.

In the given figure, AB is a diameter of the circle such that ∠A = 35° and ∠Q = 25°, find ∠PBR.

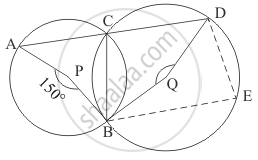
In the given figure, P and Q are centres of two circles intersecting at B and C. ACD is a straight line. Then, ∠BQD =
If the given figure, AOC is a diameter of the circle and arc AXB = \[\frac{1}{2}\] arc BYC. Find ∠BOC.
If ABC is an arc of a circle and ∠ABC = 135°, then the ratio of arc \[\stackrel\frown{ABC}\] to the circumference is ______.
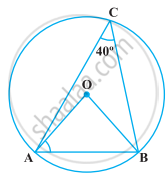
In the following figure, ∠ACB = 40º. Find ∠OAB.