Advertisements
Advertisements
Question
If O is the centre of the circle, find the value of x in the following figure:

Solution
∠AOC= 135°
∴∠AOC+ ∠BOC -180°
⇒ 135° + ∠BOC = 180°
⇒∠BOC = 180° -135° = 45°
By degree measures theorem
∠BOC = 2∠CDB
⇒ 45° = 2x
`⇒x=(45°)/2=22(1°)/2.`
APPEARS IN
RELATED QUESTIONS
Given an arc of a circle, show how to complete the circle.
If O is the centre of the circle, find the value of x in the following figures.

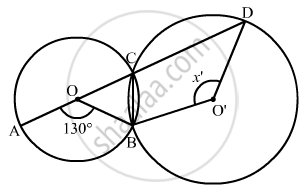
In the given figure, O and O' are centres of two circles intersecting at B and C. ACD is a straight line, find x.
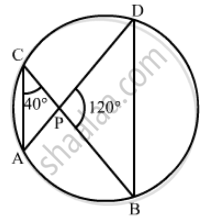
In the given figure, if ∠ACB = 40°, ∠DPB = 120°, find ∠CBD.
Prove that the angle in a segment shorter than a semicircle is greater than a right angle.
Prove that the angle in a segment greater than a semi-circle is less than a right angle.
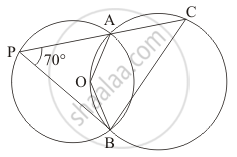
In the given figure, two circles intersect at A and B. The centre of the smaller circle is Oand it lies on the circumference of the larger circle. If ∠APB = 70°, find ∠ACB.
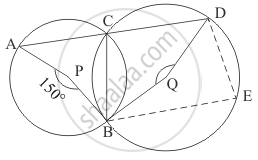
In the given figure, P and Q are centres of two circles intersecting at B and C. ACD is a straight line. Then, ∠BQD =
If ABC is an arc of a circle and ∠ABC = 135°, then the ratio of arc \[\stackrel\frown{ABC}\] to the circumference is ______.
If arcs AXB and CYD of a circle are congruent, find the ratio of AB and CD.
