Advertisements
Advertisements
Question
In the given figure, it is given that O is the centre of the circle and ∠AOC = 150°. Find ∠ABC.

Solution
It is given that O is the centre of circle and A, B and C are points on circumference.
`angle AOC = 150°` (Given)
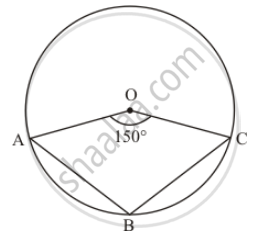
We have to find ∠ABC
The angle subtended by an arc of a circle at the centre is double the angle subtended by it at any point on the remaining part of the circle.
\[\angle ABC = \frac{1}{2}\left( \text{ reflex } \angle AOC \right)\]
\[ = \frac{1}{2}\left( 360° - 150° \right)\]
\[ = \frac{1}{2} \times 210° \]
\[ = 105° \]
Hence,`angle ABC = 105°`
APPEARS IN
RELATED QUESTIONS
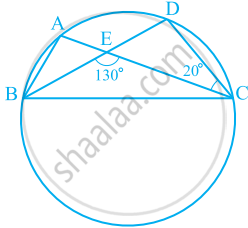
In the given figure, A, B, C and D are four points on a circle. AC and BD intersect at a point E such that ∠BEC = 130° and ∠ECD = 20°. Find ∠BAC.
Prove that the line joining the mid-point of a chord to the centre of the circle passes through the mid-point of the corresponding minor arc.
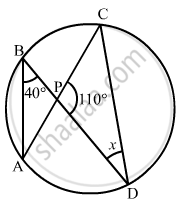
If O is the centre of the circle, find the value of x in the following figure

If O is the centre of the circle, find the value of x in the following figures.
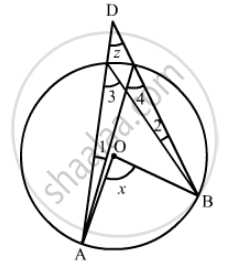
In the given figure, O is the centre of the circle, prove that ∠x = ∠y + ∠z.
Prove that the angle in a segment shorter than a semicircle is greater than a right angle.
In the given figure, two congruent circles with centres O and O' intersect at A and B. If ∠AOB = 50°, then find ∠APB.

In the given figure, AB is a diameter of the circle such that ∠A = 35° and ∠Q = 25°, find ∠PBR.

A chord of a circle is equal to its radius. Find the angle subtended by this chord at a point in major segment.
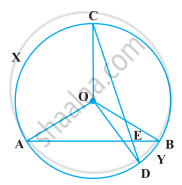
In the following figure, AB and CD are two chords of a circle intersecting each other at point E. Prove that ∠AEC = `1/2` (Angle subtended by arc CXA at centre + angle subtended by arc DYB at the centre).