Question

A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.

Answer 1

We have to find   `angleADB` and  `angle AEB`

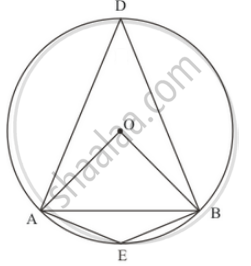
Construction: - O is centre and r is radius and given that chord is equal to radius of circle

Now in  ΔAOB we have

AO = OB = BA       ( It is given that chord is equal to radius of circle)

So,  ΔAOB  is an equilateral triangle

`angleAOB = 60°`

So,

\[\angle AOB = 2\angle ADB\]   

  (The angle subtended by an arc of a circle at the centre is double the angle subtended by it at any point on the remaining part of the circle)

Then `angleADB = 30°` 

So,

\[\angle AEB = \frac{1}{2}\left( \text{ Reflex } \angle AOB \right)\]
\[ = \frac{1}{2}\left( 360° - 60° \right)\]
\[ = 150° \]

Therefore,

`angleADB = 30°`   and `angleAEB = 150°` 

Hence, the angle subtended by the chord at a point on the minor arc is 150° and also at a point on the major arc is 30°.