Advertisements
Advertisements
Question
In the given figure, two congruent circles with centres O and O' intersect at A and B. If ∠AOB = 50°, then find ∠APB.

Solution
Since both the circles are congruent, they will have equal radii. Let their radii be ‘r’.
So, from the given figure we have,
OA = OB = O'A = O'B = r
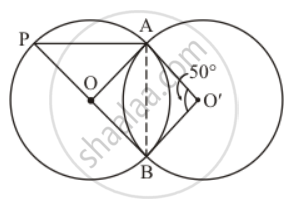
Now, since all the sides of the quadrilateral OBO’A are equal it has to be a rhombus.
One of the properties of a rhombus is that the opposite angles are equal to each other.
So, since it is given that`angle AO'B ` = 50° , we can say that the angle opposite it, that is to say that `angle AOB ` should also have the same value.
Hence we get `angle AOB ` = 50°
Now, consider the first circle with the centre ‘O’ alone. ‘AB’ forms a chord and it subtends an angle of 50° with its centre, that is .`angle AOB ` = 50°
A property of a circle is that the angle subtended by an arc at the centre of the circle is double the angle subtended by the arc in the remaining part of the circle.
This means that,
`angle APB = (angleAOB)/2`
`=(50°)/2`
= 25°
Hence the measure of `angleAPB ` is 25°
APPEARS IN
RELATED QUESTIONS
In the below fig. O is the centre of the circle. Find ∠BAC.
If O is the centre of the circle, find the value of x in the following figure

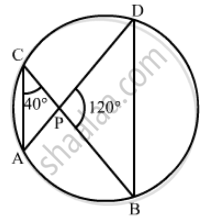
In the given figure, if ∠ACB = 40°, ∠DPB = 120°, find ∠CBD.
In the given figure, it is given that O is the centre of the circle and ∠AOC = 150°. Find ∠ABC.

In the given figure, O is the centre of a circle and PQ is a diameter. If ∠ROS = 40°, find ∠RTS.
Prove that the angle in a segment greater than a semi-circle is less than a right angle.
In the given figure, two circles intersect at A and B. The centre of the smaller circle is Oand it lies on the circumference of the larger circle. If ∠APB = 70°, find ∠ACB.
In the given figure, if ∠AOB = 80° and ∠ABC = 30°, then find ∠CAO.

If arcs AXB and CYD of a circle are congruent, find the ratio of AB and CD.
In the following figure, ∠ACB = 40º. Find ∠OAB.