Advertisements
Advertisements
प्रश्न
In the given figure, two congruent circles with centres O and O' intersect at A and B. If ∠AOB = 50°, then find ∠APB.

उत्तर
Since both the circles are congruent, they will have equal radii. Let their radii be ‘r’.
So, from the given figure we have,
OA = OB = O'A = O'B = r
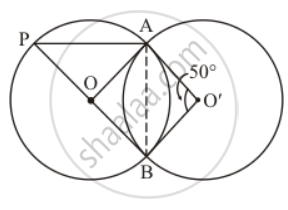
Now, since all the sides of the quadrilateral OBO’A are equal it has to be a rhombus.
One of the properties of a rhombus is that the opposite angles are equal to each other.
So, since it is given that`angle AO'B ` = 50° , we can say that the angle opposite it, that is to say that `angle AOB ` should also have the same value.
Hence we get `angle AOB ` = 50°
Now, consider the first circle with the centre ‘O’ alone. ‘AB’ forms a chord and it subtends an angle of 50° with its centre, that is .`angle AOB ` = 50°
A property of a circle is that the angle subtended by an arc at the centre of the circle is double the angle subtended by the arc in the remaining part of the circle.
This means that,
`angle APB = (angleAOB)/2`
`=(50°)/2`
= 25°
Hence the measure of `angleAPB ` is 25°
APPEARS IN
संबंधित प्रश्न
Prove that a diameter of a circle which bisects a chord of the circle also bisects the angle subtended by the chord at the centre of the circle.
Given an arc of a circle, show how to complete the circle.
If O is the centre of the circle, find the value of x in the following figure

If O is the centre of the circle, find the value of x in the following figure
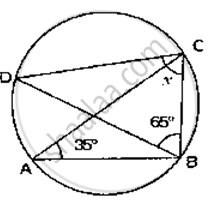
If O is the centre of the circle, find the value of x in the following figures.
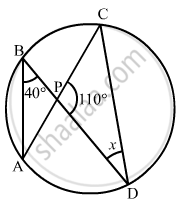
If O is the centre of the circle, find the value of x in the following figures.

O is the circumcentre of the triangle ABC and OD is perpendicular on BC. Prove that ∠BOD = ∠A
In the given figure, O is the centre of the circle, prove that ∠x = ∠y + ∠z.
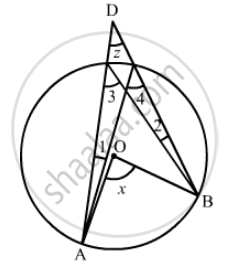
Prove that the line segment joining the mid-point of the hypotenuse of a right triangle to its opposite vertex is half the hypotenuse.
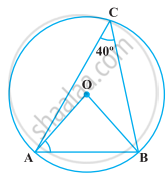
In the following figure, ∠ACB = 40º. Find ∠OAB.