Advertisements
Advertisements
प्रश्न
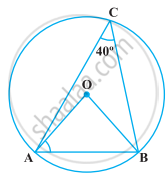
In the following figure, ∠ACB = 40º. Find ∠OAB.
उत्तर
Given, ∠ACB = 40°
We know that, a segment subtends an angle to the circle is half the angle subtends to the centre.
∴ ∠AOB = 2∠ACB
⇒ `∠ACB = (∠AOB)/2`
⇒ `40^circ = 1/2`∠AOB
⇒ ∠AOB = 80° ...(i) [Both are the radius of a circle]
In ΔAOB, AO = BO
⇒ ∠OBA = ∠OAB ...(ii) [Angles opposite to the equal sides are equal]
We know that, the sum of all three angles in a triangle AOB is 180°.
∴ ∠AOB + ∠OBA + ∠OAB = 180°
⇒ 80° + ∠OAB + ∠OAB = 180° ...[From equations (i) and (ii)]
⇒ 2∠OAB = 180° – 80°
⇒ 2∠OAB = 100°
∴ ∠OAB = `100^circ/2` = 50°
APPEARS IN
संबंधित प्रश्न
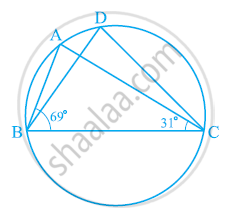
In the given figure, ∠ABC = 69°, ∠ACB = 31°, find ∠BDC.
Fill in the blank:
A circle divides the plane, on which it lies, in ............ parts.
Given an arc of a circle, complete the circle.
If O is the centre of the circle, find the value of x in the following figure

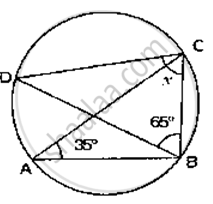
If O is the centre of the circle, find the value of x in the following figure
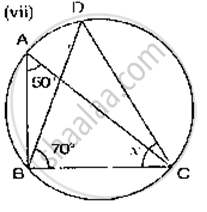
If O is the centre of the circle, find the value of x in the following figure
In the given figure, AB is a diameter of the circle such that ∠A = 35° and ∠Q = 25°, find ∠PBR.

If arcs AXB and CYD of a circle are congruent, find the ratio of AB and CD.
In the following figure, AB and CD are two chords of a circle intersecting each other at point E. Prove that ∠AEC = `1/2` (Angle subtended by arc CXA at centre + angle subtended by arc DYB at the centre).
A circle has radius `sqrt(2)` cm. It is divided into two segments by a chord of length 2 cm. Prove that the angle subtended by the chord at a point in major segment is 45°.
