Advertisements
Advertisements
प्रश्न
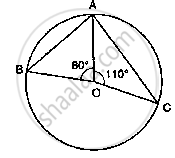
If O is the centre of the circle, find the value of x in the following figure

उत्तर
We have
∠OAB = 35°
Then, ∠OBA = ∠OAB = 35°
In ∠AOB, by angle sum property
⇒∠AOB + ∠OAB + ∠OBA = 180°
⇒ ∠AOB = 180° - 35° - 35° = 110°
∴∠AOB + reflex ∠AOB = 360°
⇒ 110° + reflex ∠AOB = 360°
⇒ reflex ∠AOB = 360° -110° = 250°
By degree measure theorem reflex ∠AOB = 2
⇒250° = 2x
`⇒ x =( 250°)/2= 125°`
APPEARS IN
संबंधित प्रश्न
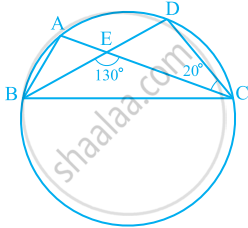
In the given figure, A, B, C and D are four points on a circle. AC and BD intersect at a point E such that ∠BEC = 130° and ∠ECD = 20°. Find ∠BAC.
In the below fig. O is the centre of the circle. Find ∠BAC.
If O is the centre of the circle, find the value of x in the following figure:

If O is the centre of the circle, find the value of x in the following figure

If O is the centre of the circle, find the value of x in the following figure

If O is the centre of the circle, find the value of x in the following figure

In the given figure, if ∠AOB = 80° and ∠ABC = 30°, then find ∠CAO.

If the given figure, AOC is a diameter of the circle and arc AXB = \[\frac{1}{2}\] arc BYC. Find ∠BOC.
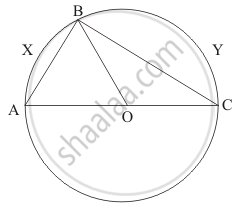
If ABC is an arc of a circle and ∠ABC = 135°, then the ratio of arc \[\stackrel\frown{ABC}\] to the circumference is ______.
A circle has radius `sqrt(2)` cm. It is divided into two segments by a chord of length 2 cm. Prove that the angle subtended by the chord at a point in major segment is 45°.
