Advertisements
Advertisements
प्रश्न
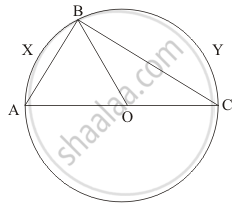
If the given figure, AOC is a diameter of the circle and arc AXB = \[\frac{1}{2}\] arc BYC. Find ∠BOC.
उत्तर
We need to find `angle BOC`

\[\text{ arc } AXB = \frac{1}{2}\text{ arc} BYC, \]
\[\angle AOB = \frac{1}{2}\angle BOC\]
\[\text{ Also } \angle AOB + \angle BOC = 180°\]
\[\text{ Therefore, } \frac{1}{2}\angle BOC + \angle BOC = 180° \]
\[ \Rightarrow \angle BOC = \frac{2}{3} \times 180°= 120°\]
APPEARS IN
संबंधित प्रश्न
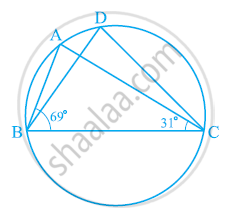
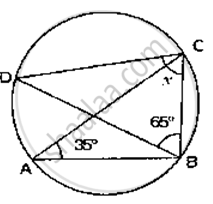
In the given figure, ∠ABC = 69°, ∠ACB = 31°, find ∠BDC.
If O is the centre of the circle, find the value of x in the following figure:

If O is the centre of the circle, find the value of x in the following figure

If O is the centre of the circle, find the value of x in the following figure

If O is the centre of the circle, find the value of x in the following figure

If O is the centre of the circle, find the value of x in the following figure
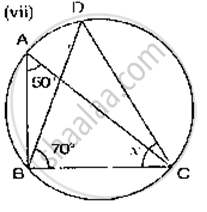
If O is the centre of the circle, find the value of x in the following figure
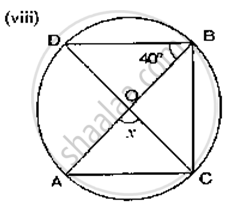
If O is the centre of the circle, find the value of x in the following figure
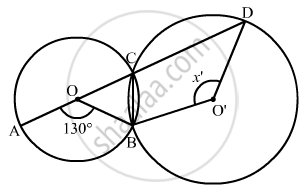
In the given figure, O and O' are centres of two circles intersecting at B and C. ACD is a straight line, find x.
Prove that the angle in a segment greater than a semi-circle is less than a right angle.
