Topics
Number Systems
Number Systems
Polynomials
Algebra
Coordinate Geometry
Linear Equations in Two Variables
Geometry
Coordinate Geometry
Introduction to Euclid’S Geometry
Mensuration
Statistics and Probability
Lines and Angles
- Introduction to Lines and Angles
- Basic Terms and Definitions
- Intersecting Lines and Non-intersecting Lines
- Introduction to Parallel Lines
- Pairs of Angles
- Parallel Lines and a Transversal
- Angle Sum Property of a Triangle
Triangles
- Concept of Triangles
- Congruence of Triangles
- Criteria for Congruence of Triangles
- Properties of a Triangle
- Some More Criteria for Congruence of Triangles
- Inequalities in a Triangle
Quadrilaterals
- Concept of Quadrilaterals
- Properties of a Quadrilateral
- Types of Quadrilaterals
- Another Condition for a Quadrilateral to Be a Parallelogram
- Theorem of Midpoints of Two Sides of a Triangle
- Property: The Opposite Sides of a Parallelogram Are of Equal Length.
- Theorem: A Diagonal of a Parallelogram Divides It into Two Congruent Triangles.
- Theorem : If Each Pair of Opposite Sides of a Quadrilateral is Equal, Then It is a Parallelogram.
- Property: The Opposite Angles of a Parallelogram Are of Equal Measure.
- Theorem: If in a Quadrilateral, Each Pair of Opposite Angles is Equal, Then It is a Parallelogram.
- Property: The diagonals of a parallelogram bisect each other. (at the point of their intersection)
- Theorem : If the Diagonals of a Quadrilateral Bisect Each Other, Then It is a Parallelogram
Circles
Areas - Heron’S Formula
Surface Areas and Volumes
Statistics
Algebraic Expressions
Algebraic Identities
Area
Constructions
- Introduction of Constructions
- Basic Constructions
- Some Constructions of Triangles
Probability
Notes
If two chords of a circle are equal, then their corresponding arcs are congruent and conversely, if two arcs are congruent, then their corresponding chords are equal. In following fig.
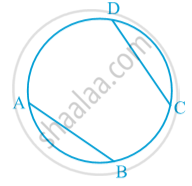
Conversely, If two arcs are equal or congruent then their corresponding chords are equal.
AB ≅ CD
`=>` AB = CD
Theorem
Theorem: The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
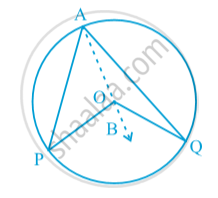
If in a circle with centre O , arc PQ of a circle subtends ∠POQ at centre and arc PQ subtends ∠PAQ on the remaining part of the circle than ∠POQ = 2 PAQ.
Theorem: Angles in the same segment of a circle are equal.
Suppose we join points P and Q and form a chord PQ in the above figures. Then ∠ PAQ is also called the angle formed in the segment PAQP.

∠ POQ = 2 ∠ PCQ = 2 ∠ PAQ
Therefore, ∠ PCQ = ∠ PAQ.
Here ∠PAQ is an angle in the segment, which is a semicircle. Also, ∠ PAQ = `1/2`
∠POQ = `1/2 xx = 180° =90° `
Theorem: If a line segment joining two points subtends equal angles at two other points lying on the same side of the line containing the line segment, the four points lie on a circle (i.e. they are concyclic).
In following fig. AB is a line segment, which subtends equal angles at two points C and D. That is ∠ ACB = ∠ ADB
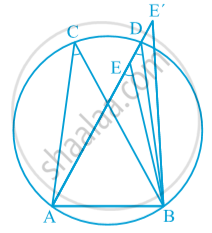
To show that the points A, B, C and D lie on a circle. let us draw a circle through the points A, C and B. Suppose it does not pass through the point D. Then it will intersect AD (or extended AD) at a point, say E .
If points A, C, E and B lie on a circle,
∠ ACB = ∠ AEB
But it is given that ∠ ACB = ∠ ADB.
Therefore, ∠ AEB = ∠ ADB.
This is not possible unless E coincides with D.
Similarly, E′ should also coincide with D.
Shaalaa.com | Theorem : The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
Series:
00:13:32 undefined
00:06:29 undefined
00:06:06 undefined