Topics
Number Systems
Number Systems
Polynomials
Algebra
Coordinate Geometry
Linear Equations in Two Variables
Geometry
Coordinate Geometry
Introduction to Euclid’S Geometry
Mensuration
Statistics and Probability
Lines and Angles
- Introduction to Lines and Angles
- Basic Terms and Definitions
- Intersecting Lines and Non-intersecting Lines
- Introduction to Parallel Lines
- Pairs of Angles
- Parallel Lines and a Transversal
- Angle Sum Property of a Triangle
Triangles
- Concept of Triangles
- Congruence of Triangles
- Criteria for Congruence of Triangles
- Properties of a Triangle
- Some More Criteria for Congruence of Triangles
- Inequalities in a Triangle
Quadrilaterals
- Concept of Quadrilaterals
- Properties of a Quadrilateral
- Types of Quadrilaterals
- Another Condition for a Quadrilateral to Be a Parallelogram
- Theorem of Midpoints of Two Sides of a Triangle
- Property: The Opposite Sides of a Parallelogram Are of Equal Length.
- Theorem: A Diagonal of a Parallelogram Divides It into Two Congruent Triangles.
- Theorem : If Each Pair of Opposite Sides of a Quadrilateral is Equal, Then It is a Parallelogram.
- Property: The Opposite Angles of a Parallelogram Are of Equal Measure.
- Theorem: If in a Quadrilateral, Each Pair of Opposite Angles is Equal, Then It is a Parallelogram.
- Property: The diagonals of a parallelogram bisect each other. (at the point of their intersection)
- Theorem : If the Diagonals of a Quadrilateral Bisect Each Other, Then It is a Parallelogram
Circles
Areas - Heron’S Formula
Surface Areas and Volumes
Statistics
Algebraic Expressions
Algebraic Identities
Area
Constructions
- Introduction of Constructions
- Basic Constructions
- Some Constructions of Triangles
Probability
Notes
Take a line segment PQ and a point R not on the line containing PQ. Join PR and QR (see following Fig.).
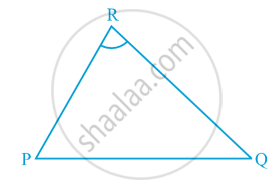
Then ∠ PRQ is called the angle subtended by the line segment PQ at the point R. What are angles POQ, PRQ and PSQ called in following Fig.
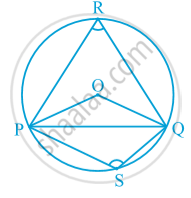
∠ POQ is the angle subtended by the chord PQ at the centre O,
∠ PRQ and ∠ PSQ are respectively the angles subtended by PQ at points R and S on the major and minor arcs PQ.
There different chords of a circle and angles subtended by them at the centre that the longer is the chord, the bigger will be the angle subtended by it at the centre.
Draw two or more equal chords of a circle and measure the angles subtended by them at the centre.
Theorem
Theorem: Equal chords of a circle subtend equal angles at the centre.
Proof : You are given two equal chords AB and CD of a circle with centre O (see following Fig.). You want to prove that ∠ AOB = ∠ COD.
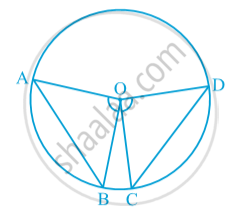
In triangles AOB and COD,
OA = OC (Radii of a circle)
OB = OD (Radii of a circle)
AB = CD (Given) Therefore, ∆ AOB ≅ ∆ COD (SSS rule) This gives ∠ AOB = ∠ COD
(Corresponding parts of congruent triangles)
Theorem: If the angles subtended by the chords of a circle at the centre are equal, then the chords are equal.
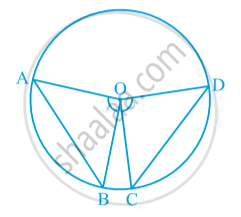
Given : ∠AOB = ∠ POQ
To prove : AB = PQ
Proof: In triangles AOB and POQ,
∠AOB = ∠POQ (Given)
OA =OP (Radii of same circle)
OB = OQ (Radii of same circle)
∆ AOB ≅ ∆ POQ (SAS congruence rule)
AB = PQ (CPCT)
Hence , the theorem is proved.

