Advertisements
Advertisements
प्रश्न
O is the circumcentre of the triangle ABC and OD is perpendicular on BC. Prove that ∠BOD = ∠A
उत्तर
We have to prove that ∠BOD = ∠A
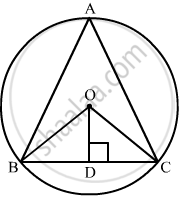
Since, circumcenter is the intersection of perpendicular bisectors of each side of the triangle.
Now according to figure A, B, C are the vertices of ΔABC
In ΔBOC , OD is perpendicular bisector of BC
So, BD = CD
OB = OC (Radius of the same circle)
And,
OD = OD (Common)
Therefore,
We know that angle formed any chord of the circle at the center is twice of the angle formed at the circumference by same chord
Therefore,
` angleBAC = 1/2 angleBOC`
`⇒ angleBAC = 1/2 xx 2 angleBOD`
`⇒ angleBAC = angle BOD`
Therefore,
`angleBOD = angleA`
Hence proved
APPEARS IN
संबंधित प्रश्न
Fill in the blank:
Segment of a circle is the region between an arc and .................. of the circle.
Fill in the blank:
A circle divides the plane, on which it lies, in ............ parts.
Given an arc of a circle, show how to complete the circle.
If O is the centre of the circle, find the value of x in the following figure

In the given figure, O is the centre of the circle, BO is the bisector of ∠ABC. Show that AB = BC.
In the given figure, it is given that O is the centre of the circle and ∠AOC = 150°. Find ∠ABC.

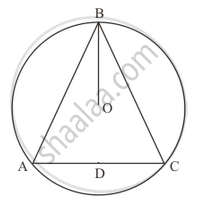
In the given figure, two circles intersect at A and B. The centre of the smaller circle is Oand it lies on the circumference of the larger circle. If ∠APB = 70°, find ∠ACB.
In the given figure, A is the centre of the circle. ABCD is a parallelogram and CDE is a straight line. Find ∠BCD : ∠ABE.

A chord of a circle is equal to its radius. Find the angle subtended by this chord at a point in major segment.
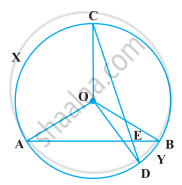
In the following figure, AB and CD are two chords of a circle intersecting each other at point E. Prove that ∠AEC = `1/2` (Angle subtended by arc CXA at centre + angle subtended by arc DYB at the centre).