Advertisements
Advertisements
प्रश्न
In the given figure, O is the centre of the circle, BO is the bisector of ∠ABC. Show that AB = BC.
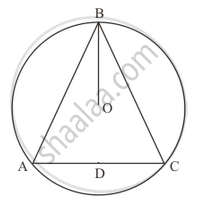
उत्तर
It is given that,∠ABC is on circumference of circle BD is passing through centre.

Construction: Join A and C to form AC and extend BO to D such that BD be the perpendicular bisector of AC.
Now in
AD = CD (BD is the perpendicular bisector)
So ,
APPEARS IN
संबंधित प्रश्न
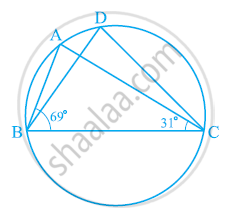
In the given figure, ∠ABC = 69°, ∠ACB = 31°, find ∠BDC.
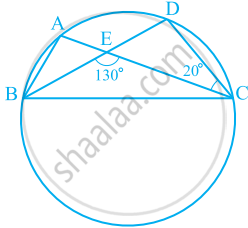
In the given figure, A, B, C and D are four points on a circle. AC and BD intersect at a point E such that ∠BEC = 130° and ∠ECD = 20°. Find ∠BAC.
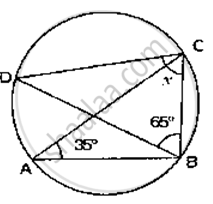
If O is the centre of the circle, find the value of x in the following figure

If O is the centre of the circle, find the value of x in the following figure
O is the circumcentre of the triangle ABC and OD is perpendicular on BC. Prove that ∠BOD = ∠A
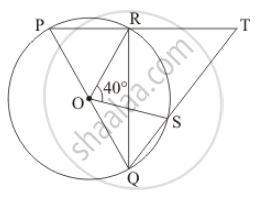
In the given figure, O is the centre of a circle and PQ is a diameter. If ∠ROS = 40°, find ∠RTS.
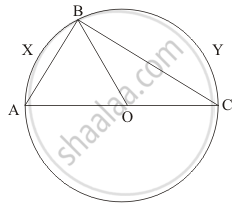
Prove that the line segment joining the mid-point of the hypotenuse of a right triangle to its opposite vertex is half the hypotenuse.
If the given figure, AOC is a diameter of the circle and arc AXB =
If ABC is an arc of a circle and ∠ABC = 135°, then the ratio of arc
The chord of a circle is equal to its radius. The angle subtended by this chord at the minor arc of the circle is
