Advertisements
Advertisements
Question
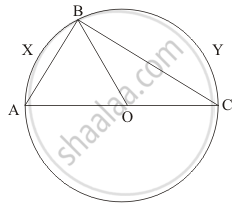
In the given figure, O is the centre of the circle, BO is the bisector of ∠ABC. Show that AB = BC.
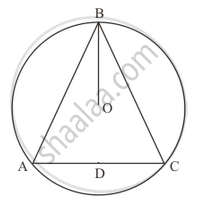
Solution
It is given that,∠ABC is on circumference of circle BD is passing through centre.

Construction: Join A and C to form AC and extend BO to D such that BD be the perpendicular bisector of AC.
Now in \[\bigtriangleup BDA \text{ and } \bigtriangleup BDC\] we have
AD = CD (BD is the perpendicular bisector)
So ,
APPEARS IN
RELATED QUESTIONS
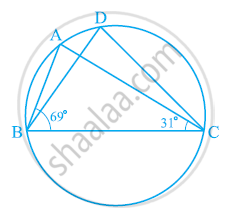
In the given figure, ∠ABC = 69°, ∠ACB = 31°, find ∠BDC.
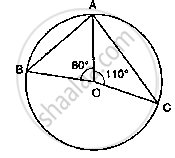
In the below fig. O is the centre of the circle. Find ∠BAC.
If O is the centre of the circle, find the value of x in the following figures.

O is the circumcentre of the triangle ABC and OD is perpendicular on BC. Prove that ∠BOD = ∠A
In the given figure, it is given that O is the centre of the circle and ∠AOC = 150°. Find ∠ABC.

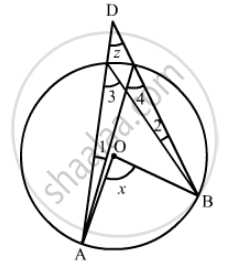
In the given figure, O is the centre of the circle, prove that ∠x = ∠y + ∠z.
In the given figure, AB is a diameter of the circle such that ∠A = 35° and ∠Q = 25°, find ∠PBR.

If the given figure, AOC is a diameter of the circle and arc AXB = \[\frac{1}{2}\] arc BYC. Find ∠BOC.
In a circle, the major arc is 3 times the minor arc. The corresponding central angles and the degree measures of two arcs are
A circle has radius `sqrt(2)` cm. It is divided into two segments by a chord of length 2 cm. Prove that the angle subtended by the chord at a point in major segment is 45°.
