Advertisements
Advertisements
Question
In a circle, the major arc is 3 times the minor arc. The corresponding central angles and the degree measures of two arcs are
Options
90° and 270°
90° and 90°
270° and 90°
60° and 210°
Advertisements
Solution
270° and 90°
We are given the major arc is 3 times the minor arc. We are asked to find the corresponding central angle.
See the corresponding figure.
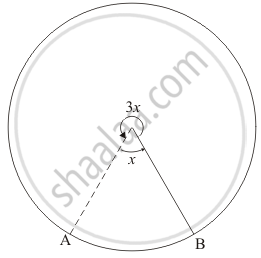
We know that angle formed by the circumference at the centre is 360°.
Since the circumference of the circle is divided into two parts such that the angle formed by major and minor arcs at the centre are 3x and x respectively.
So 3x + x = 360
4x = 360
x = 90
So m \[\stackrel\frown{AB}\] = 90° and m \[\stackrel\frown{AB}\] = 3x = 270°
APPEARS IN
RELATED QUESTIONS
In the given figure, ∠ABC = 69°, ∠ACB = 31°, find ∠BDC.
If O is the centre of the circle, find the value of x in the following figure
If O is the centre of the circle, find the value of x in the following figures.
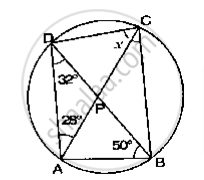
If O is the centre of the circle, find the value of x in the following figures.
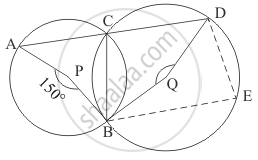
O is the circumcentre of the triangle ABC and OD is perpendicular on BC. Prove that ∠BOD = ∠A.
In the given figure, O is the centre of the circle, prove that ∠x = ∠y + ∠z.
Prove that the angle in a segment shorter than a semicircle is greater than a right angle.
Prove that the angle in a segment greater than a semi-circle is less than a right angle.
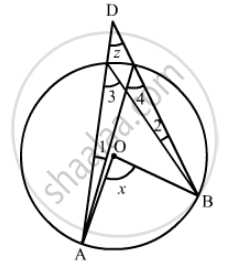
In the given figure, if ∠AOB = 80° and ∠ABC = 30°, then find ∠CAO.
In the given figure, AB is a diameter of the circle such that ∠A = 35° and ∠Q = 25°, find ∠PBR.
