Advertisements
Advertisements
प्रश्न
In a circle, the major arc is 3 times the minor arc. The corresponding central angles and the degree measures of two arcs are
विकल्प
90° and 270°
90° and 90°
270° and 90°
60° and 210°
उत्तर
270° and 90°
We are given the major arc is 3 times the minor arc. We are asked to find the corresponding central angle.
See the corresponding figure.
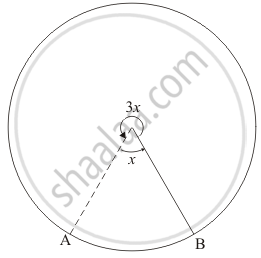
We know that angle formed by the circumference at the centre is 360°.
Since the circumference of the circle is divided into two parts such that the angle formed by major and minor arcs at the centre are 3x and x respectively.
So 3x + x = 360
4x = 360
x = 90
So m \[\stackrel\frown{AB}\] = 90° and m \[\stackrel\frown{AB}\] = 3x = 270°
APPEARS IN
संबंधित प्रश्न
Fill in the blank:
A circle divides the plane, on which it lies, in ............ parts.
Prove that the line joining the mid-point of a chord to the centre of the circle passes through the mid-point of the corresponding minor arc.
If O is the centre of the circle, find the value of x in the following figure

In the given figure, it is given that O is the centre of the circle and ∠AOC = 150°. Find ∠ABC.

In the given figure, two congruent circles with centres O and O' intersect at A and B. If ∠AOB = 50°, then find ∠APB.

In the given figure, AB is a diameter of the circle such that ∠A = 35° and ∠Q = 25°, find ∠PBR.

The chord of a circle is equal to its radius. The angle subtended by this chord at the minor arc of the circle is
If arcs AXB and CYD of a circle are congruent, find the ratio of AB and CD.
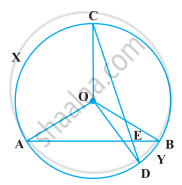
In the following figure, AB and CD are two chords of a circle intersecting each other at point E. Prove that ∠AEC = `1/2` (Angle subtended by arc CXA at centre + angle subtended by arc DYB at the centre).
A circle has radius `sqrt(2)` cm. It is divided into two segments by a chord of length 2 cm. Prove that the angle subtended by the chord at a point in major segment is 45°.
