Advertisements
Advertisements
Question
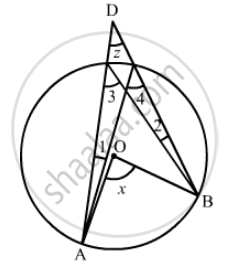
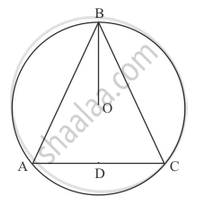
In the given figure, O is the centre of the circle, prove that ∠x = ∠y + ∠z.
Solution
It is given that, O is the center of circle and A, B and C are points on circumference on triangle
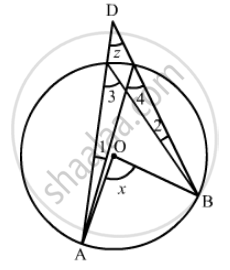
We have to prove that ∠x = ∠y + ∠z
∠4 and ∠3 are on same segment
So, ∠4 = ∠3
`angle x = 2 angle3` (Angle subtended by an arc of a circle at the centre is double the angle subtended by it at any point on the remaining part of the circle)
`anglex = angle 4 + angle 3` …… (1)
`angley= angle 3 + angle 1` (Exterior angle is equal to the sum of two opposite interior angles) …… (2)
(Exterior angle is equal to the sum of two opposite interior angles)
`anglez= angle 4 - angle 1` …… (3)
Adding (2) and (3)
`angley + angle z = angle 3 + angle 4` ……(4)
From equation (1) and (4) we have
`anglex = angle y + angle z`
APPEARS IN
RELATED QUESTIONS
Fill in the blank:
Segment of a circle is the region between an arc and .................. of the circle.
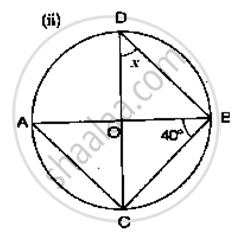
If O is the centre of the circle, find the value of x in the following figure:
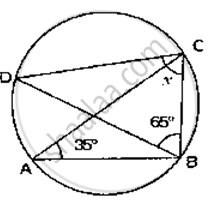
If O is the centre of the circle, find the value of x in the following figure
O is the circumcentre of the triangle ABC and OD is perpendicular on BC. Prove that ∠BOD = ∠A
In the given figure, O is the centre of the circle, BO is the bisector of ∠ABC. Show that AB = BC.
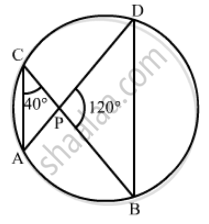
In the given figure, if ∠ACB = 40°, ∠DPB = 120°, find ∠CBD.
In the given figure, if ∠AOB = 80° and ∠ABC = 30°, then find ∠CAO.

In the given figure, AB is a diameter of the circle such that ∠A = 35° and ∠Q = 25°, find ∠PBR.

In the given figure, if O is the circumcentre of ∠ABC, then find the value of ∠OBC + ∠BAC.

If ABC is an arc of a circle and ∠ABC = 135°, then the ratio of arc \[\stackrel\frown{ABC}\] to the circumference is ______.
