Advertisements
Advertisements
Question
In the given figure, O is the centre of a circle and PQ is a diameter. If ∠ROS = 40°, find ∠RTS.
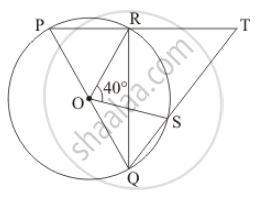
Solution
It is given that O is the centre and \[\angle ROS = 40° \]

We have `angle RQS = 1/2 angle ROS = 20°`
In right angled triangle RQT we have
\[\angle RQT + \angle QTR + \angle TRQ = 180° \]
\[ \Rightarrow 20° + \angle QTR + 90° = 180° \]
\[ \Rightarrow \angle QTR = 70° \]
APPEARS IN
RELATED QUESTIONS
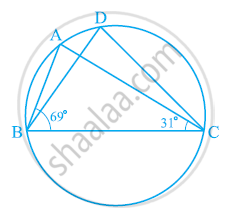
In the given figure, ∠ABC = 69°, ∠ACB = 31°, find ∠BDC.
Fill in the blank:
A circle divides the plane, on which it lies, in ............ parts.
If O is the centre of the circle, find the value of x in the following figure:

If O is the centre of the circle, find the value of x in the following figure

In the given figure, two congruent circles with centres O and O' intersect at A and B. If ∠AOB = 50°, then find ∠APB.

In the given figure, A is the centre of the circle. ABCD is a parallelogram and CDE is a straight line. Find ∠BCD : ∠ABE.

In the given figure, AB is a diameter of the circle such that ∠A = 35° and ∠Q = 25°, find ∠PBR.

In a circle, the major arc is 3 times the minor arc. The corresponding central angles and the degree measures of two arcs are
The chord of a circle is equal to its radius. The angle subtended by this chord at the minor arc of the circle is
If arcs AXB and CYD of a circle are congruent, find the ratio of AB and CD.
