Advertisements
Advertisements
प्रश्न
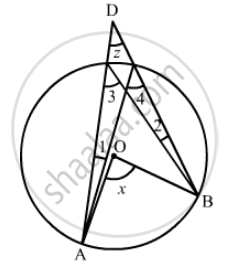
In the given figure, O is the centre of the circle, prove that ∠x = ∠y + ∠z.
उत्तर
It is given that, O is the center of circle and A, B and C are points on circumference on triangle
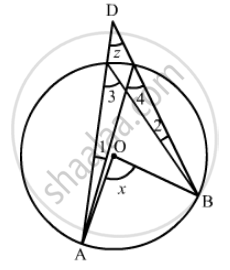
We have to prove that ∠x = ∠y + ∠z
∠4 and ∠3 are on same segment
So, ∠4 = ∠3
`angle x = 2 angle3` (Angle subtended by an arc of a circle at the centre is double the angle subtended by it at any point on the remaining part of the circle)
`anglex = angle 4 + angle 3` …… (1)
`angley= angle 3 + angle 1` (Exterior angle is equal to the sum of two opposite interior angles) …… (2)
(Exterior angle is equal to the sum of two opposite interior angles)
`anglez= angle 4 - angle 1` …… (3)
Adding (2) and (3)
`angley + angle z = angle 3 + angle 4` ……(4)
From equation (1) and (4) we have
`anglex = angle y + angle z`
APPEARS IN
संबंधित प्रश्न
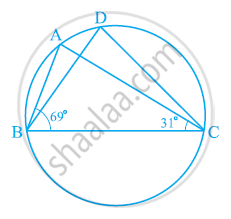
In the given figure, ∠ABC = 69°, ∠ACB = 31°, find ∠BDC.
If O is the centre of the circle, find the value of x in the following figure:

If O is the centre of the circle, find the value of x in the following figure

If O is the centre of the circle, find the value of x in the following figure

If O is the centre of the circle, find the value of x in the following figure
If O is the centre of the circle, find the value of x in the following figure
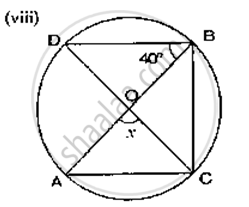
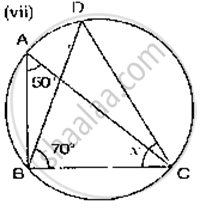
If O is the centre of the circle, find the value of x in the following figures.

In the given figure, A is the centre of the circle. ABCD is a parallelogram and CDE is a straight line. Find ∠BCD : ∠ABE.

The chord of a circle is equal to its radius. The angle subtended by this chord at the minor arc of the circle is
A circle has radius `sqrt(2)` cm. It is divided into two segments by a chord of length 2 cm. Prove that the angle subtended by the chord at a point in major segment is 45°.
