Advertisements
Advertisements
प्रश्न
If ABC is an arc of a circle and ∠ABC = 135°, then the ratio of arc \[\stackrel\frown{ABC}\] to the circumference is ______.
पर्याय
1 : 4
3 : 4
3 : 8
1 : 2
उत्तर
If ABC is an arc of a circle and ∠ABC = 135°, then the ratio of arc \[\stackrel\frown{ABC}\] to the circumference is 3 : 8.
Explanation:
∠ABC = 135°
ABC is an arc
Circumference = 360°
Arc = 135°
`(Arc ABC)/(Circumference) = 135/360`
= `3/8`
APPEARS IN
संबंधित प्रश्न
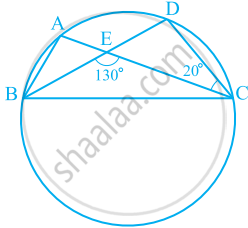
In the given figure, A, B, C and D are four points on a circle. AC and BD intersect at a point E such that ∠BEC = 130° and ∠ECD = 20°. Find ∠BAC.
Fill in the blank:
Segment of a circle is the region between an arc and .................. of the circle.
Given an arc of a circle, complete the circle.
In the below fig. O is the centre of the circle. Find ∠BAC.
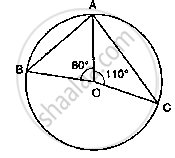
If O is the centre of the circle, find the value of x in the following figure

If O is the centre of the circle, find the value of x in the following figure
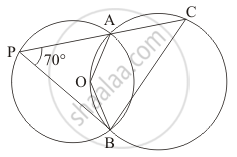
In the given figure, two circles intersect at A and B. The centre of the smaller circle is Oand it lies on the circumference of the larger circle. If ∠APB = 70°, find ∠ACB.
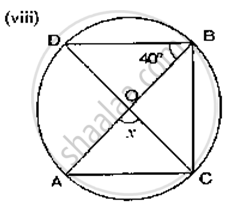
In the given figure, two congruent circles with centres O and O' intersect at A and B. If ∠AOB = 50°, then find ∠APB.

In the given figure, P and Q are centres of two circles intersecting at B and C. ACD is a straight line. Then, ∠BQD =
A chord of a circle is equal to its radius. Find the angle subtended by this chord at a point in major segment.
