Advertisements
Advertisements
प्रश्न
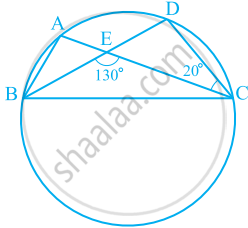
In the given figure, A, B, C and D are four points on a circle. AC and BD intersect at a point E such that ∠BEC = 130° and ∠ECD = 20°. Find ∠BAC.
उत्तर
In ΔCDE,
∠CDE + ∠DCE = ∠CEB ...(Exterior angle)
⇒ ∠CDE + 20° = 130°
⇒ ∠CDE = 110°
However, ∠BAC = ∠CDE ...(Angles in the same segment of a circle)
⇒ ∠BAC = 110°
APPEARS IN
संबंधित प्रश्न
If O is the centre of the circle, find the value of x in the following figure

If O is the centre of the circle, find the value of x in the following figure
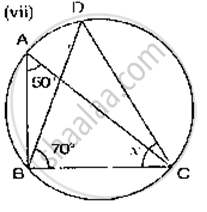
If O is the centre of the circle, find the value of x in the following figure
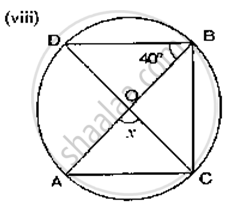
In the given figure, it is given that O is the centre of the circle and ∠AOC = 150°. Find ∠ABC.

Prove that the line segment joining the mid-point of the hypotenuse of a right triangle to its opposite vertex is half the hypotenuse.
In the given figure, two congruent circles with centres O and O' intersect at A and B. If ∠AOB = 50°, then find ∠APB.

In the given figure, if O is the circumcentre of ∠ABC, then find the value of ∠OBC + ∠BAC.

If ABC is an arc of a circle and ∠ABC = 135°, then the ratio of arc \[\stackrel\frown{ABC}\] to the circumference is ______.
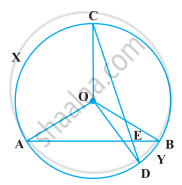
If arcs AXB and CYD of a circle are congruent, find the ratio of AB and CD.
In the following figure, AB and CD are two chords of a circle intersecting each other at point E. Prove that ∠AEC = `1/2` (Angle subtended by arc CXA at centre + angle subtended by arc DYB at the centre).