Advertisements
Advertisements
प्रश्न
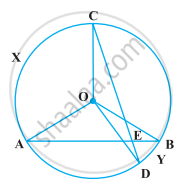
In the following figure, AB and CD are two chords of a circle intersecting each other at point E. Prove that ∠AEC = `1/2` (Angle subtended by arc CXA at centre + angle subtended by arc DYB at the centre).
उत्तर
Given: In a figure, two chords AB and CD intersecting each other at point E.
To prove: ∠AEC = `1/2` ...[Angle subtended by arc C × A at centre + angle subtended by arc DYB at the centre]
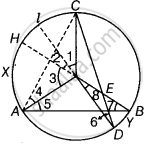
Construction: Extend the line DO and BO at the points l and H on the circle. Also, join AC.
Proof: We know that, in a circle, the angle subtended by an arc at the centre is twice the angle subtended by it at the remaining part of the circle.
∴ ∠1 = 2∠6 ...(i)
And ∠3 = 2∠7 ...(ii)
In ΔAOC, OC = OA ...[Both are the radius of circle]
∠OCA = ∠4 ...[Angles opposite to equal sides are equal]
Also, ∠AOC + ∠OCA + ∠4 = 180° ...[By angle sum property of triangle]
⇒ ∠AOC + ∠4 + ∠4 = 180°
⇒ ∠AOC = 180° – 2∠4 ...(iii)
Now, in ΔAEC, ∠AEC + ∠ECA + ∠CAE = 180° ...[By angle property sum of a triangle]
⇒ ∠AEC = 180° – (∠ECA + ∠CAE)
⇒ ∠AEC = 180° – [(∠ECO + ∠OCA) + ∠CAO + ∠OAE]
= 180° – (∠6 + ∠4 + ∠4 + ∠5) ...[In ΔOCD, ∠6 = ∠ECO angles opposites to equal sides are equal]
= 180° – (2∠4 + ∠5 + ∠6)
= 180° – (180° – ∠AOC + ∠7 + ∠6) ...[From equation (iii) and in ΔAOB, ∠5 = ∠7, as (angles opposite to equal sides are equal)]
= `∠AOC - (∠3)/2 - (∠1)/2` ...[From equations (i) and (ii)]
= `∠AOC - (∠1)/2 - (∠2)/2 - (∠3)/2 + (∠2)/2` ...`["Adding and subtracting" (∠2)/2]`
= `∠AOC - 1/2 (∠1 + ∠2 + ∠3) + (∠8)/2` ...[∵ ∠2 = ∠8 vertically opposite angles]
= `∠AOC - (∠AOC)/2 + (∠DOB)/2`
⇒ `∠AEC = 1/2(∠AOC + ∠DOB)`
= `1/2` ...[Angle subtended by arc CXA at the centre + angle subtended by arc DYB at the centre]
APPEARS IN
संबंधित प्रश्न
Fill in the blank:
Segment of a circle is the region between an arc and .................. of the circle.
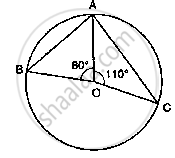
In the below fig. O is the centre of the circle. Find ∠BAC.
If O is the centre of the circle, find the value of x in the following figure

If O is the centre of the circle, find the value of x in the following figure
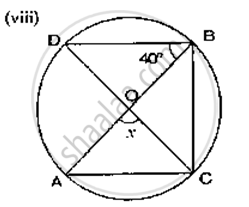
If O is the centre of the circle, find the value of x in the following figures.

In the given figure, it is given that O is the centre of the circle and ∠AOC = 150°. Find ∠ABC.

In the given figure, if O is the circumcentre of ∠ABC, then find the value of ∠OBC + ∠BAC.

If arcs AXB and CYD of a circle are congruent, find the ratio of AB and CD.
A chord of a circle is equal to its radius. Find the angle subtended by this chord at a point in major segment.
A circle has radius `sqrt(2)` cm. It is divided into two segments by a chord of length 2 cm. Prove that the angle subtended by the chord at a point in major segment is 45°.
