Advertisements
Advertisements
प्रश्न
If ABC is an equilateral triangle inscribed in a circle and P be any point on the minor arc BC which does not coincide with B or C, prove that PA is angle bisector of ∠BPC.
उत्तर
Given: ΔABC is an equilateral triangle inscribed in a circle and P be any point on the minor arc BC which does not coincide with B or C.
To prove: PA is an angle bisector of ∠BPC.
Construction: Join PB and PC.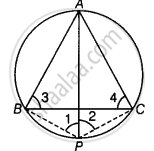
Proof: Since, ΔABC is an equilateral triangle.
∠3 = ∠4 = 60°
Now, ∠1 = ∠4 = 60° ...(i) [Angles in the same segment AB]
∠2 = ∠3 = 60° ...(ii) [Angles in the same segment AC]
∴ ∠1 = ∠2 = 60°
Hence, PA is the bisector of ∠BPC.
Hence proved.
APPEARS IN
संबंधित प्रश्न
Write True or False. Give reason for your answer.
A circle has only finite number of equal chords.
Write True or False. Give reasons for your answers.
If a circle is divided into three equal arcs, each is a major arc.
Fill in the blank:
An arc is a ................ when its ends are the ends of a diameter.
In the following figure, AB is the diameter of a circle with centre O and CD is the chord with length equal to radius OA.
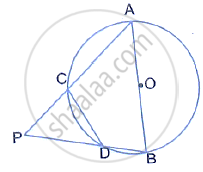
Is AC produced and BD produced meet at point P; show that ∠APB = 60°
A point P is 25 cm away from the center of a circle and the length of tangent drawn from P to the circle is 24 cm. Find the radius of the circle.
If the difference between the circumference and the radius of a circle is 37 cm, then using`22/7`, the circumference (in cm) of the circle is:
In the given figure, chords AD and BC intersect each other at right angles at a point P. If ∠DAB = 35°, then

If a line segment joining mid-points of two chords of a circle passes through the centre of the circle, prove that the two chords are parallel.
From the figure, identify a point in the exterior.

Assertion (A): If the circumference of a circle is 176 cm, then its radius is 28 cm.
Reason (R): Circumference = 2π × radius of a circle.
