Advertisements
Advertisements
प्रश्न
A point P is 25 cm away from the center of a circle and the length of tangent drawn from P to the circle is 24 cm. Find the radius of the circle.
उत्तर
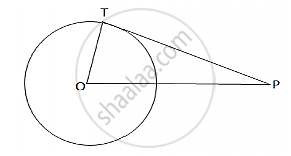
Draw a circle and let P be a point such that OP = 25cm.
Let TP be the tangent, so that TP = 24cm
Join OT where OT is radius.
Now, tangent drawn from an external point is perpendicular to the radius at the point of contact.
∴ OT ⊥ PT
In the right Δ OTP,we have:
`OP^2 = OT^2 +TP^2 ` [By Pythagoras’ theorem:]
`OT^2 = sqrt(OP^2 - TP^2 )`
`=sqrt(25^2 - 24^2`
`= sqrt(625-576)`
`=sqrt(49)`
= 7 cm
∴ The length of the radius is 7cm.
APPEARS IN
संबंधित प्रश्न
In the fig. ABC is right triangle right angled at B such that BC = 6cm and AB = 8cm. Find the radius of its in circle.
In the fig. a circle is inscribed in a quadrilateral ABCD in which ∠B = 90° if AD = 23cm,
AB = 29cm and DS = 5cm, find the radius of the circle.
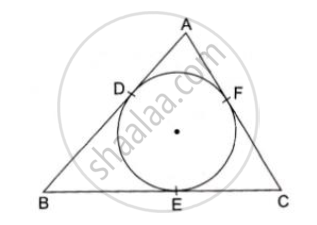
In the given figure, a circle inscribed in a triangle ABC, touches the sides AB, BC and AC at points D, E and F Respectively. If AB= 12cm, BC=8cm and AC = 10cm, find the length of AD, BE and CF.
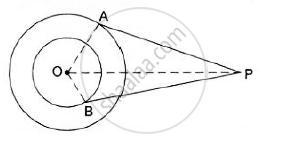
In the given figure, O is the centre of the two concentric circles of radii 4 cm and 6cm respectively. AP and PB are tangents to the outer and inner circle respectively. If PA = 10cm, find the length of PB up to one place of the decimal.
In the given figure, ABCD is a cyclic quadrilateral. If ∠BCD = 100° and ∠ABD = 70°, find ∠ADB.

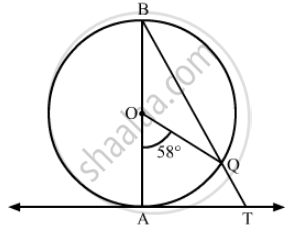
In the given figure, AB is a diameter of a circle with centre O and AT is a tangent. If \[\angle\] AOQ = 58º, find \[\angle\] ATQ.
Find the length of the chord of a circle in the following when:
Radius is 6.5 cm and the distance from the centre is 2.5 cm
Draw a circle of radius of 4.2 cm. Mark its center as O. Takes a point A on the circumference of the circle. Join AO and extend it till it meets point B on the circumference of the circle,
(i) Measure the length of AB.
(ii) Assign a special name to AB.
Draw circle with diameter: 8.4 cm
In above case, measure the length of the radius of the circle drawn.
A chord is 12 cm away from the centre of the circle of radius 15 cm. Find the length of the chord
