Advertisements
Advertisements
प्रश्न
A chord is 12 cm away from the centre of the circle of radius 15 cm. Find the length of the chord
उत्तर
Radius of a circle (OA) = 15 cm
Distance from centre to the chord (OC) = 12 cm
In the right ΔOAC,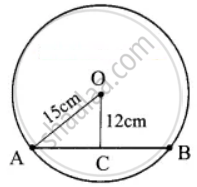
AC2 = OA2 – OC2
= 152 – 122
= 225 – 144
= 81
AC = `sqrt(81)`
= 9
Length of the chord (AB)
= AC + CB
= 9 + 9
= 18 cm.
APPEARS IN
संबंधित प्रश्न
If ΔABC is isosceles with AB = AC and C (0, 2) is the in circle of the ΔABC touching BC at L, prove that L, bisects BC.
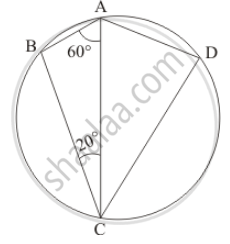
In the given figure, if ∠BAC = 60° and ∠BCA = 20°, find ∠ADC.

In the above figure, `square`XLMT is a rectangle. LM = 21 cm, XL = 10.5 cm. Diameter of the smaller semicircle is half the diameter of the larger semicircle. Find the area of non-shaded region.
Use the figure given below to fill in the blank:
________ is a radius of the circle.
Find the diameter of the circle
Radius = 6 cm
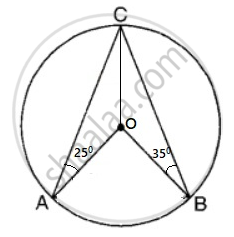
In the adjoining figure ‘O’ is the center of the circle, ∠CAO = 25° and ∠CBO = 35°. What is the value of ∠AOB?
A point P is 10 cm from the center of a circle. The length of the tangent drawn from P to the circle is 8 cm. The radius of the circle is equal to ______
The tangent to the circumcircle of an isosceles triangle ABC at A, in which AB = AC, is parallel to BC.
If A, B, C and D are four points such that ∠BAC = 45° and ∠BDC = 45°, then A, B, C, D are concyclic.
Say true or false:
The centre of a circle is always in its interior.
