Advertisements
Advertisements
प्रश्न

In the above figure, `square`XLMT is a rectangle. LM = 21 cm, XL = 10.5 cm. Diameter of the smaller semicircle is half the diameter of the larger semicircle. Find the area of non-shaded region.
उत्तर
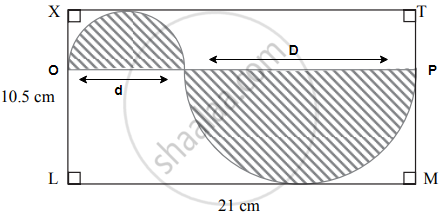
Given: `square`XLMT is a rectangle.
LM = XT and XL = TM .....(Opposite sides are equal)
∴ XT = 21 cm
TM = 10.5 cm
To find the area of a non-shaded region
The diameter of a smaller semicircle is half the diameter of a larger semi-circle.
Let the diameter of the larger semicircle is D and the diameter of the smaller semicircle be `1/2 xx D = D/2`.
Now, the diameter of the smaller semicircle + the diameter of the larger semicircle = 21 cm
`D + D/2 = 21`
`(2D + D)/2 = 21`
`(3D)/2 = 21`
`3D = 21 xx 2`
`D = (21 xx 2)/3`
D = 14
A(smaller semi-circle) = `1/2 pir^2`
= `1/2 xx 22/7 xx 7/2 xx 7/2`
= `77/4 "cm"^2`
A(largerer semi-circle) = `1/2pir^2`
`= 1/2 xx 22/7 xx 14/2 xx 14/2`
= `77 "cm"^2`
A(`square`XLMT) = length × breadth
= LM × XL
= 21 cm × 10.5 cm
= 220.5 cm2
Area of the non-shaded region
= A(`square`XLMT) – A(smaller semi-circle) – A(larger semi-circle)
= 220.5 – `77/4 - 77`
= 220.5 – 19.25 – 77
= 124.25 cm2
APPEARS IN
संबंधित प्रश्न
In Fig. 1, PA and PB are tangents to the circle with centre O such that ∠APB = 50°. Write the measure of ∠OAB.

Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
Prove that in two concentric circles, the chord of the larger circle which touches the smaller circle, is bisected at the point of contact.
In the given figure, PQ and RS are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersects PQ at A and RS at B. Prove that ∠AOB = 90º
A chord PQ of a circle of radius 10 cm substends an angle of 60° at the centre of circle. Find the area of major and minor segments of the circle.
In the given figure, PA and PB are the tangent segemtns to a circle with centre O. Show that he points A, O, B and P are concyclic.

PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T. Find the lengths of TP and TQ.

In Fig. 4, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that the point of contact P bisects the base BC.
Length of a chord of a circle is 24 cm. If distance of the chord from the centre is 5 cm, then the radius of that circle is ______.
Use the figure given below to fill in the blank:
Diameter of a circle is ______.

Draw a circle of radius 3.6 cm. In the circle, draw a chord AB = 5 cm. Now shade the minor segment of the circle.
Can the length of a chord of a circle be greater than its diameter ? Explain.
In figure, AB is a chord of the circle and AOC is its diameter such that ∠ACB = 50°. If AT is the tangent to the circle at point A, then ∠BAT is equal to ______.
If a number of circles touch a given line segment PQ at a point A, then their centres lie on the perpendicular bisector of PQ.
If a hexagon ABCDEF circumscribe a circle, prove that AB + CD + EF = BC + DE + FA.
If AB = 12 cm, BC = 16 cm and AB is perpendicular to BC, then the radius of the circle passing through the points A, B and C is ______.
If ABC is an equilateral triangle inscribed in a circle and P be any point on the minor arc BC which does not coincide with B or C, prove that PA is angle bisector of ∠BPC.
From the figure, identify a chord.

Is every diameter of a circle also a chord?
The circumcentre of a triangle is the point which is ______.
