Advertisements
Advertisements
प्रश्न
A chord PQ of a circle of radius 10 cm substends an angle of 60° at the centre of circle. Find the area of major and minor segments of the circle.
उत्तर

Radius of the circle, r = 10 cm
Area of sector OPRQ
`= 60^@/360^@ xx pir^2`
`= 1/6 xx 3.14 xx (10)^2`
`= 52.33 cm^3`
In ΔOPQ,
∠OPQ = ∠OQP (As OP = OQ)
∠OPQ + ∠OQP + ∠POQ = 180°
2∠OPQ = 120°
∠OPQ = 60°
ΔOPQ is an equilateral triangle.
So, area of ΔOPQ
`= sqrt3/4 xx ("Side")^2`
`= sqrt3/4 xx (10)^2`
`=( 100sqrt3)/4 cm^2`
=43.30 cm2
Area of minor segment PRQ
= Area of sector OPRQ − Area of ΔOPQ
= 52.33 − 43.30
= 9.03 cm2
Area of major segment PSQ
= Area of circle − Area of minor segment PRQ
=π(10)2 − 9.03
=314 − 9.03
= 304.97 cm2
APPEARS IN
संबंधित प्रश्न
Write True or False. Give reason for your answer.
Sector is the region between the chord and its corresponding arc.
The circumference of a circle is 22 cm. The area of its quadrant (in cm2) is
The center of a circle is at point O and its radius is 8 cm. State the position of a point P (point P may lie inside the circle, on the circumference of the circle, or outside the circle), when:
(a) OP = 10.6 cm
(b) OP = 6.8 cm
(c) OP = 8 cm
Draw a circle of diameter 7 cm. Draw two radii of this circle such that the angle between these radii is 90°. Shade the minor sector obtained. Write a special name for this sector.
State, if the following statement is true or false:
The longest chord of a circle is its diameter.
The ______________ is the longest chord of a circle
Circles with centres A, B and C touch each other externally. If AB = 36, BC = 32, CA = 30, then find the radii of each circle.
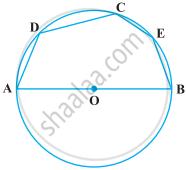
In the following figure, if AOB is a diameter and ∠ADC = 120°, then ∠CAB = 30°.
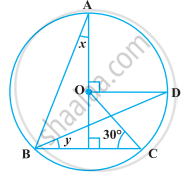
In the following figure, O is the centre of the circle, ∠BCO = 30°. Find x and y.
From the figure, identify a chord.

