Advertisements
Advertisements
प्रश्न
Circles with centres A, B and C touch each other externally. If AB = 36, BC = 32, CA = 30, then find the radii of each circle.
उत्तर
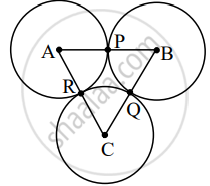
Given: AB = 36, BC = 32, CA = 30
To Find: Radii of each circle.
Solution:
Let x, y, z be the radii of the circles with centers A, B, C respectively.
∴ AP = RA = x, PB = BQ = y, CR = QC = z
AB = AP + PB ....[A–P–B]
∴ 36 = x + y ...(ii) [From (i) and given]
BC = BQ + QC ....[B – Q – C]
∴ 32 = y + z .....(iii) [From (i) and given]
CA = CR + RA ......[C – R – A]
∴ 30 = z + x ......(iv) [From (i) and given]
Now,
AB + BC + CA = 36 + 32 + 30
∴ (AP + PB) + (BQ + QC) + (CR + RA) = 98 ......[A–P–B, B–Q–C, C–R–A]
∴ (x + y) + (y + z) + (z + x) = 98 ......[From (i)]
∴ 2x + 2y + 2z = 98
∴ 2(x + y + z) = 98
∴ x + y + z = `98/2`
∴ x + y + z = 49
∴ (x + y) + z = 49 .....[From (ii)]
∴ 36 + z = 49
∴ z = 49 – 36
∴ z = 13 ......(v)
y + z = 32 ......[From (iii)]
∴ y + 13 = 32 ......[From (v)]
∴ y = 32 – 13
∴ y = 19
z + x = 30 .....[From (iv)]
∴ 13 + x = 30 .....[From (v)]
∴ x = 30 – 13
∴ x = 17
APPEARS IN
संबंधित प्रश्न
In the fig. ABC is right triangle right angled at B such that BC = 6cm and AB = 8cm. Find the radius of its in circle.
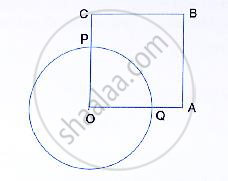
In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC
at P and OA at Q. Prove that:
(i) ΔOPA ≅ ΔOQC, (ii) ΔBPC ≅ ΔBQA.
In the given figure, AB is a side of a regular six-sided polygon and AC is a side of a regular eight-sided polygon inscribed in the circle with centre O. Calculate the sizes of:
- ∠AOB,
- ∠ACB,
- ∠ABC.
In the given figure, a circle with center O, is inscribed in a quadrilateral ABCD such that it touches the side BC, AB, AD and CD at points P, Q, R and S respectively. If AB = 29cm, AD = 23cm, ∠B = 90° and DS=5cm then find the radius of the circle.

In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 60° then find the measure of ∠OAB.

Find the length of the chord of a circle in the following when:
Radius is 1. 7cm and the distance from the centre is 1.5 cm
In the given figure, O is the centre of a circle, chord PQ ≅ chord RS If ∠ POR = 70° and (arc RS) = 80°, find –
(1) m(arc PR)
(2) m(arc QS)
(3) m(arc QSR)

Use the figure given below to fill in the blank:
EF is a ______ of the circle.

Draw circle with the radii given below.
2 cm
The radius of a circle of diameter 24 cm is _______
Find the missing values in the following table for the circles with radius (r), diameter (d) and Circumference (C).
| radius (r) | diameter (d) | Circumference (C) |
| 1760 cm |
Find the radius of the circle
Diameter = 30 cm
In figure, chords AC and DE intersect at B. If ∠ABE = 108°, m(arc AE) = 95°, find m(arc DC).

In the figure, segment PQ is the diameter of the circle with center O. The tangent to the tangent circle drawn from point C on it, intersects the tangents drawn from points P and Q at points A and B respectively, prove that ∠AOB = 90°
C(O, r1) and C(O, r2) are two concentric circles with r1 > r2 AB is a chord of C(O, r1) touching C(O, r2) at C then ______
If a chord AB subtends an angle of 60° at the centre of a circle, then the angle between the tangents at A and B is ______
If angle between two tangents drawn from a point P to a circle of radius a and centre O is 60°, then OP = `asqrt(3)`
The tangent to the circumcircle of an isosceles triangle ABC at A, in which AB = AC, is parallel to BC.
If AB = 12 cm, BC = 16 cm and AB is perpendicular to BC, then the radius of the circle passing through the points A, B and C is ______.
A circle of radius 3 cm with centre O and a point L outside the circle is drawn, such that OL = 7 cm. From the point L, construct a pair of tangents to the circle. Justify LM and LN are the two tangents.
