Advertisements
Advertisements
प्रश्न
If angle between two tangents drawn from a point P to a circle of radius a and centre O is 60°, then OP = `asqrt(3)`
पर्याय
True
False
उत्तर
This statement is False.
Explanation:
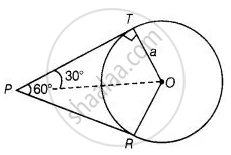
From point P, two tangents are drawn.
Given, OT = a
Also, line OP bisects the ∠RPT.
∴ ∠TPO = ∠RPO = 30°
Also, OT ⊥ PT
⇒ ∠OTP = 90°
In right angled ΔOTP,
sin 30° = `"OT"/"OP"`
⇒ `1/2 = "a"/"OP"`
⇒ OP = 2a
APPEARS IN
संबंधित प्रश्न
From a point T outside a circle of centre O, tangents TP and TQ are drawn to the circle. Prove that OT is the right bisector of line segment PQ.
Suppose You Are Given a Circle. Give a Construction to Find Its Centre.
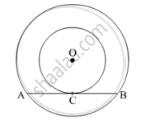
In Fig. 5, the chord AB of the larger of the two concentric circles, with centre O, touches the smaller circle at C. Prove that AC = CB.
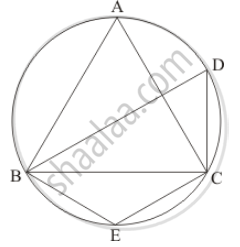
In the given figure, if ABC is an equilateral triangle. Find ∠BDC and ∠BEC.
In the given figure, O is the centre of the circle and BCD is tangent to it at C. Prove that ∠BAC + ∠ACD = 90°.

A part of circumference of a circle is called as _______
All the radii of a circle are _______________
Circles with centres A, B and C touch each other externally. If AB = 3 cm, BC = 3 cm, CA = 4 cm, then find the radii of each circle.
In the following figure, ∠ADC = 130° and chord BC = chord BE. Find ∠CBE.

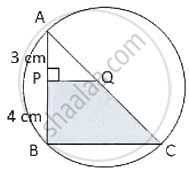
In the adjoining figure, AC is a diameter of the circle. AP = 3 cm and PB = 4 cm and QP ⊥ AB. If the area of ΔAPQ is 18 cm2, then the area of shaded portion QPBC is ______.