Advertisements
Advertisements
Question
If angle between two tangents drawn from a point P to a circle of radius a and centre O is 60°, then OP = `asqrt(3)`
Options
True
False
Solution
This statement is False.
Explanation:
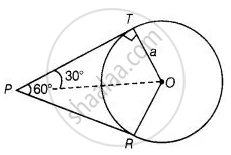
From point P, two tangents are drawn.
Given, OT = a
Also, line OP bisects the ∠RPT.
∴ ∠TPO = ∠RPO = 30°
Also, OT ⊥ PT
⇒ ∠OTP = 90°
In right angled ΔOTP,
sin 30° = `"OT"/"OP"`
⇒ `1/2 = "a"/"OP"`
⇒ OP = 2a
APPEARS IN
RELATED QUESTIONS
From a point T outside a circle of centre O, tangents TP and TQ are drawn to the circle. Prove that OT is the right bisector of line segment PQ.
In the given figure, PQ is a chord of length 8cm of a circle of radius 5cm. The tangents at P and Q intersect at a point T. Find the length TP

Two tangent segments PA and PB are drawn to a circle with center O such that ∠APB =120°. Prove that OP = 2AP
In the given figure, AB is a chord of length 16 cm of a circle of radius 10 cm. The tangents at A and B intersect at a point P. Find the length of PA.
true or false
Sector is the region between the chord and its corresponding arc.
O is the centre of a circle of radius 10 cm. P is any point in the circle such that OP = 6 cm. A is the point travelling along the circumference. x is the distance from A to P. what are the least and the greatest values of x in cm? what is the position of the points O, P and A at these values?
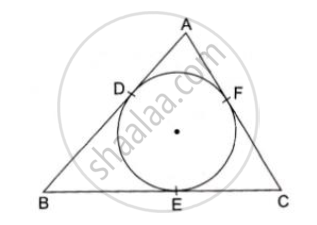
In the given figure, a circle inscribed in a triangle ABC, touches the sides AB, BC and AC at points D, E and F Respectively. If AB= 12cm, BC=8cm and AC = 10cm, find the length of AD, BE and CF.
Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
On a semi-circle with AB as diameter, a point C is taken, so that m (∠CAB) = 30°. Find m(∠ACB) and m (∠ABC).
Find the missing values in the following table for the circles with radius (r), diameter (d) and Circumference (C).
| radius (r) | diameter (d) | Circumference (C) |
| 24 m |
