Advertisements
Advertisements
Question
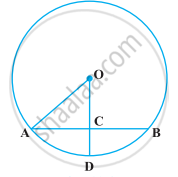
Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
Solution

Suppose CD and AB are two parallel tangents of a circle with center O
Construction: Draw a line parallel to CD passing through O i.e. OP
We know that the radius and tangent are perpendicular at their point of contact.
∠OQC = ∠ORA = 90°
Now, ∠OQC + ∠POQ = 180° (co-interior angles)
⇒ ∠POQ = 180° - 90° = 90°
Similarly, Now, ∠ORA +∠POR =180° (co-interior angles)
⇒ ∠POQ = 180° - 90° = 90°
Now,∠POR + ∠POQ = 90° + 90° =180°
Since, ∠POR and ∠POQare linear pair angles whose sum is 180°
Hence, QR is a straight line passing through center O.
APPEARS IN
RELATED QUESTIONS
Prove that the line segment joining the point of contact of two parallel tangents to a circle is a diameter of the circle.
Find the length of the tangent drawn from a point whose distance from the centre of a circle is 25 cm. Given that the radius of the circle is 7 cm.
In Fig., if AB = AC, prove that BE = EC
PA and PB are tangents from P to the circle with centre O. At point M, a tangent is drawn cutting PA at K and PB at N. Prove that KN = AK + BN.
In the given figure, if ∠ABC = 45°, then ∠AOC =
If all the sides of a parallelogram touch a circle, show that the parallelogram is a rhombus.
State, if the following statement is true or false:
If the end points A and B of the line segment lie on the circumference of a circle, AB is a diameter.
A part of circumference of a circle is called as _______
The tangent to the circumcircle of an isosceles triangle ABC at A, in which AB = AC, is parallel to BC.
In the following figure, if OA = 5 cm, AB = 8 cm and OD is perpendicular to AB, then CD is equal to ______.