Advertisements
Advertisements
Question
If all the sides of a parallelogram touch a circle, show that the parallelogram is a rhombus.
Solution
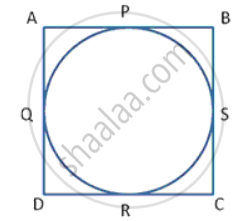
Let the sides of parallelogram ABCD touch the circle at points P, Q, R and S.
AP = AS - (1)
PB = BQ - {2} {Length of tangents drawn from an external point to a circle a equal)
DR = DS - {3}
RC = CQ - (4)
Adding (1), {2}, {3} and (4)
AP + PB + DR + RC = AS + BQ + DS + CQ
AB + CD = AD + BC
2 AB = 2 BC => AB = BC {Opposite sides of a parallelogram are equal)
:. AB = BC = CD = DA,
Hence , ABCD is a rhombus.
APPEARS IN
RELATED QUESTIONS
In Fig. 1, QR is a common tangent to the given circles, touching externally at the point T. The tangent at T meets QR at P. If PT = 3.8 cm, then the length of QR (in cm) is :
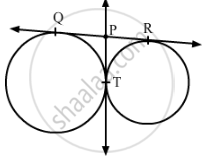
(A) 3.8
(B) 7.6
(C) 5.7
(D) 1.9
Fill in the blanks:
The longest chord of a circle is a __________ of the circle.
In fig. a circle touches all the four sides of quadrilateral ABCD with AB = 6cm, BC = 7cm, CD = 4cm. Find AD.
Fill in the blank
Circles having the same centre and different radii are called ...........................circles.
A circle is inscribed in a ΔABC touching AB, BC and AC at P, Q and R respectively. If AB = 10 cm, AR=7cm and CR=5cm, find the length of BC.

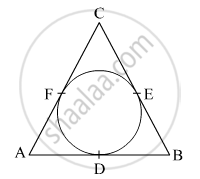
In Fig. 4, a circle inscribed in triangle ABC touches its sides AB, BC and AC at points D, E and F respectively. If AB = 12 cm, BC = 8 cm and AC = 10 cm, then find the lengths of AD, BE and CF.
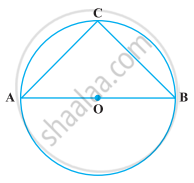
Use the figure given below to fill in the blank:
Diameter of a circle is ______.
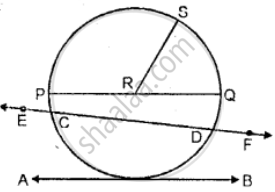
Use the figure given below to fill in the blank:
EF is a ______ of the circle.

If a chord AB subtends an angle of 60° at the centre of a circle, then the angle between the tangents at A and B is ______
In the following figure, if AOB is a diameter of the circle and AC = BC, then ∠CAB is equal to ______.