Advertisements
Advertisements
Question
In Fig. 1, QR is a common tangent to the given circles, touching externally at the point T. The tangent at T meets QR at P. If PT = 3.8 cm, then the length of QR (in cm) is :
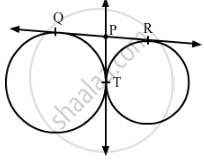
(A) 3.8
(B) 7.6
(C) 5.7
(D) 1.9
Solution

It is known that the length of the tangents drawn from an external point to a circle are equal.
∴ QP = PT = 3.8 cm ...(1)
PR = PT = 3.8 cm ...(2)
From equations (1) and (2), we get:
QP = PR = 3.8 cm
Now, QR = QP + PR
= 3.8 cm + 3.8 cm
= 7.6 cm
Hence, the correct option is B.
APPEARS IN
RELATED QUESTIONS
In Figure 1, common tangents AB and CD to the two circles with centres 01and 02 intersect at E. Prove that AB = CD.

Fill in the blanks:
The longest chord of a circle is a __________ of the circle.
Fill in the blanks:
Segment of a circle is the region between an arc and __________ of the circle.
Two circles touch externally at a point P. from a point T on the tangent at P, tangents TQ and TR are drawn to the circles with points of contact Q and E respectively. Prove that TQ = TR.
In following figure, three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these three circles (shaded region). `["Use" pi=22/7]`

AB is a chord of a circle with centre O , AOC is a diameter and AT is the tangent at A as shown in Fig . 10.70. Prove that \[\angle\]BAT = \[\angle\] ACB.
Radius of a circle with centre O is 4 cm. If l(OP) = 4.2 cm, say where point P will lie.
The figure given below shows a circle with center O in which diameter AB bisects the chord CD at point E. If CE = ED = 8 cm and EB = 4 cm,
find the radius of the circle.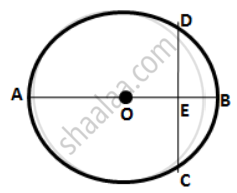
In an equilateral triangle, prove that the centroid and center of the circum-circle (circumcentre) coincide.
O is the circumcentre of the triangle ABC and D is the mid-point of the base BC. Prove that ∠BOD = ∠A.
