Advertisements
Advertisements
Question
AB is a chord of a circle with centre O , AOC is a diameter and AT is the tangent at A as shown in Fig . 10.70. Prove that \[\angle\]BAT = \[\angle\] ACB.
Solution
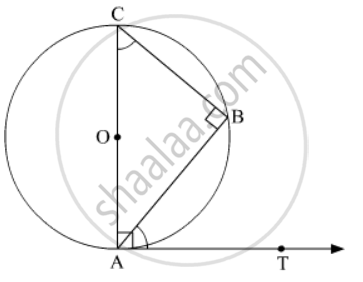
In the given figure,
AC is the diameter.
So,
AT is the tangent at point A.
Thus,
\[ \Rightarrow \angle BCA + 90^o + \angle CAT - \angle BAT = 180^o \]
\[ \Rightarrow \angle BCA + 90^o + 90 - \angle BAT = 180^o \]
\[ \Rightarrow \angle BCA = \angle BAT\]
Hence Proved
APPEARS IN
RELATED QUESTIONS
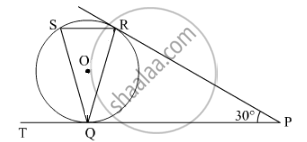
In the given figure, tangents PQ and PR are drawn from an external point P to a circle with centre O, such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find ∠RQS.
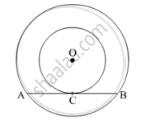
In Fig. 5, the chord AB of the larger of the two concentric circles, with centre O, touches the smaller circle at C. Prove that AC = CB.
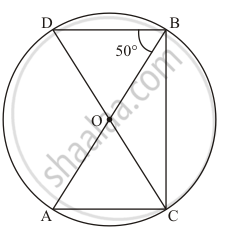
In the given figure, AB and CD are diameters of a circle with centre O. If ∠OBD = 50°, find ∠AOC.
In the given figure, ABC is a right triangle right-angled at B such that BC = 6 cm and AB = 8 cm. Find the radius of its incircle.

A triangle PQR is drawn to circumscribe a circle of radius 8 cm such that the segments QT and TR, into which QR is divided by the point of contact T, are of lengths 14 cm and 16 cm respectively. If area of ∆PQR is 336 cm2, find the sides PQ and PR.
In the given circle with diameter AB, find the value of x.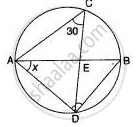
Use the figure given below to fill in the blank:
Diameter of a circle is ______.

Use the figure given below to fill in the blank:
Tangent to a circle is _______.

Construct a triangle ABC with AB = 5 cm, ∠B = 60° and BC = 6. 4 cm. Draw the incircle of the triangle ABC.
The longest chord of a circle is __________
