Advertisements
Advertisements
Question
Construct a triangle ABC with AB = 5 cm, ∠B = 60° and BC = 6. 4 cm. Draw the incircle of the triangle ABC.
Solution
Steps of Construction:
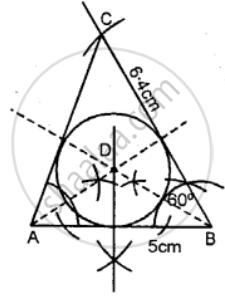
(i) Draw a line AB = 5 cm.
(ii)B as a center draw an angle with the help of compass ∠B = 60°. Cut the line with an arc BC = 6 4 cm.
(iii) Join AC.
(iv) Now, from A and B cut the bisector of ∠A and ∠B, which intersect each other at point D.
(v) With D as a centre draw an in a circle which touches all the three sides of AABC.
APPEARS IN
RELATED QUESTIONS
Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
In the given figure, BC is a tangent to the circle with centre O. OE bisects AP. Prove that ΔAEO~Δ ABC.

Fill in the blank
A continuous piece of a circle is ............... of the circle
Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
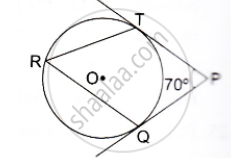
In the given figure, O is the centre of a circle. PT and PQ are tangents to the circle from an external point P. If ∠TPQ = 70° , find the ∠TRQ.
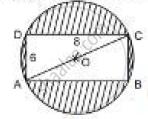
Find the area of the shaded region in the figure If ABCD is a rectangle with sides 8 cm and 6 cm and O is the centre of the circle. (Take π= 3.14)
Use the figure given below to fill in the blank:
________ is a radius of the circle.
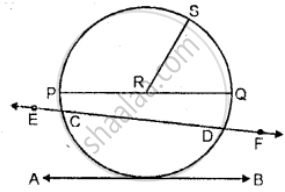
The ______________ is the longest chord of a circle
In figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find the ∠RQS.
[Hint: Draw a line through Q and perpendicular to QP.]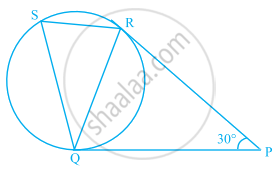
If ABC is an equilateral triangle inscribed in a circle and P be any point on the minor arc BC which does not coincide with B or C, prove that PA is angle bisector of ∠BPC.
