Advertisements
Advertisements
Question
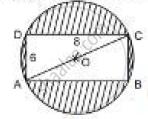
Find the area of the shaded region in the figure If ABCD is a rectangle with sides 8 cm and 6 cm and O is the centre of the circle. (Take π= 3.14)
Solution
Here, diagonal AC also represents the diameter of the circle.
Using Pythagoras theorem:
AC = `sqrt(AB^2 + BC^2)`
AC = `sqrt(8^2 + 6^2)`
AC = `sqrt(64 + 36)`
AC = `sqrt100`
AC = 10
RAdius of the circle, OC = `"AC"/2 = 5 "cm"`
Area of the shaded region = Area of the circle - Area of rectangle
= `pi"r"^2 - "AB"xx"BC"`
= `pi ("OC")^2 - "AB"xx"BC"`
= 3.14 x 52 - 8 x 6
= 78.5 - 48
= 30.5
Therefore, the area of shaded region is 30.5 cm2 .
APPEARS IN
RELATED QUESTIONS
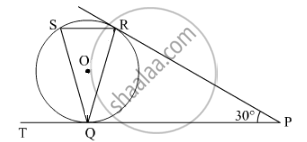
In the given figure, tangents PQ and PR are drawn from an external point P to a circle with centre O, such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find ∠RQS.
In the fig. ABC is right triangle right angled at B such that BC = 6cm and AB = 8cm. Find the radius of its in circle.
If the difference between the circumference and the radius of a circle is 37 cm, then using`22/7`, the circumference (in cm) of the circle is:
In the given figure, O is the centre of the circle. Find ∠CBD.

Find the area of a circle of radius 7 cm.
From a point P which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is ______
On a common hypotenuse AB, two right triangles ACB and ADB are situated on opposite sides. Prove that ∠BAC = ∠BDC.
In the given figure, O is the centre of the circle. Name a chord, which is not the diameter of the circle.
From the figure, identify a diameter.
Is every chord of a circle also a diameter?
