Advertisements
Advertisements
प्रश्न
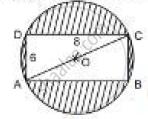
Find the area of the shaded region in the figure If ABCD is a rectangle with sides 8 cm and 6 cm and O is the centre of the circle. (Take π= 3.14)
उत्तर
Here, diagonal AC also represents the diameter of the circle.
Using Pythagoras theorem:
AC = `sqrt(AB^2 + BC^2)`
AC = `sqrt(8^2 + 6^2)`
AC = `sqrt(64 + 36)`
AC = `sqrt100`
AC = 10
RAdius of the circle, OC = `"AC"/2 = 5 "cm"`
Area of the shaded region = Area of the circle - Area of rectangle
= `pi"r"^2 - "AB"xx"BC"`
= `pi ("OC")^2 - "AB"xx"BC"`
= 3.14 x 52 - 8 x 6
= 78.5 - 48
= 30.5
Therefore, the area of shaded region is 30.5 cm2 .
APPEARS IN
संबंधित प्रश्न
ABC is a right triangle, right angled at B. A circle is inscribed in it. The lengths of the two sides containing the right angle are 6 cm and 8 cm. Find the radius of the incircle.
If from any point on the common chord of two intersecting circles, tangents be drawn to circles, prove that they are equal.
In the given figure, ΔABC is an equilateral triangle. Find m∠BEC.
In the given figure, chords AD and BC intersect each other at right angles at a point P. If ∠DAB = 35°, then

In the given figure, O is the centre of the circle and ∠BDC = 42°. The measure of ∠ACB is
If \[d_1 , d_2 ( d_2 > d_1 )\] be the diameters of two concentric circle s and c be the length of a chord of a circle which is tangent to the other circle , prove that\[{d_2}^2 = c^2 + {d_1}^2\].
In the given figure, chord EF || chord GH. Prove that, chord EG ≅ chord FH. Fill in the blanks and write the proof.

State, if the following statement is true or false:
If the end points A and B of the line segment lie on the circumference of a circle, AB is a diameter.
If AB is a chord of a circle with centre O, AOC is a diameter and AT is the tangent at A as shown in figure. Prove that ∠BAT = ∠ACB
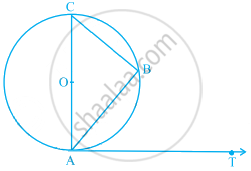
In the following figure, O is the centre of the circle, BD = OD and CD ⊥ AB. Find ∠CAB.