Advertisements
Advertisements
प्रश्न
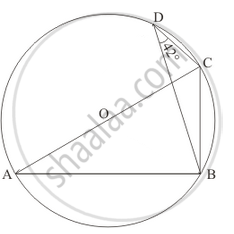
In the given figure, O is the centre of the circle and ∠BDC = 42°. The measure of ∠ACB is
पर्याय
42°
48°
58°
52°
उत्तर
48°
Construction: Join A and D.
Since AC is the diameter. So ∠ADC will be 90°.
Therefore,
`angleADB = 90 - angleBDC`
= 90 - 42
`angle ADB = 48°`
∠ACB = ∠ADB = 48° (Angle in the same segment are equal.)
APPEARS IN
संबंधित प्रश्न
If PT is a tangent at T to a circle whose center is O and OP = 17 cm, OT = 8 cm. Find the length of tangent segment PT.
In the following figure, AB is the diameter of a circle with centre O and CD is the chord with length equal to radius OA.
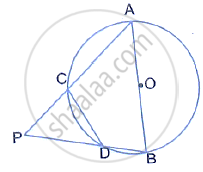
Is AC produced and BD produced meet at point P; show that ∠APB = 60°
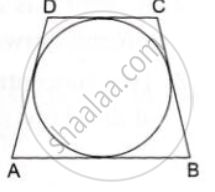
In the given figure, a circle touches all the four sides of a quadrilateral ABCD whose three sides are AB = 6cm, BC=7cm and CD=4 cm. Find AD.
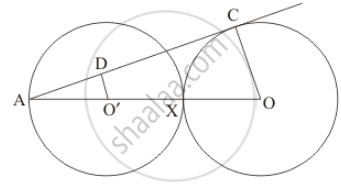
Equal circles with centres O and O' touch each other at X. OO' produced to meet a circle with centre O', at A. AC is a tangent to the circle whose centre is O. O'D is perpendicular to AC. Find the value of\[\frac{DO'}{CO}\]
Choose correct alternative answer and fill in the blank.
Radius of a circle is 10 cm and distance of a chord from the centre is 6 cm. Hence the length of the chord is .........
Find the diameter of the circle if the length of a chord is 3.2 cm and itd distance from the centre is 1.2 cm.
Draw a circle of diameter 7 cm. Draw two radii of this circle such that the angle between these radii is 90°. Shade the minor sector obtained. Write a special name for this sector.
Find the missing values in the following table for the circles with radius (r), diameter (d) and Circumference (C).
| radius (r) | diameter (d) | Circumference (C) |
| 24 m |
Find the radius of the circle
Diameter = 76 cm
In the given figure, O is the centre of the circle. Shade the smaller segment of the circle formed by CP.