Question

In a circle with centre O, AB and CD are two diameters perpendicular to each other. The length of chord AC is

पर्याय

• 2AB

• \[\sqrt{2}\]

   

• \[\frac{1}{2}AB\]

   

• \[\frac{1}{\sqrt{2}}AB\]

   

Answer 1

\[\frac{1}{\sqrt{2}}AB\]

We are given a circle with centre at O and two perpendicular diameters AB and CD.

We need to find the length of AC.

We have the following corresponding figure:

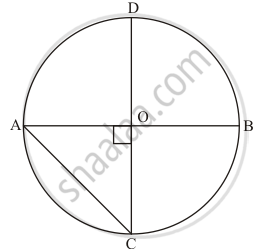
Since, AB = CD                   (Diameter of the same circle)

Also, ∠AOC = 90°

And,  AO =  `(AB)/2`

Here,  AO = OC (radius)

In ΔAOC

`AC^2 = AO^2 + OC^2 = AO^2 + AO^2`

        `= ((AB)/2)^2 + ((AB)/2)^2`

 `AC^2 = (AB^2)/2`

`AC = (AB)/(sqrt(2))`