Advertisements
Advertisements
प्रश्न
If two diameters of a circle intersect each other at right angles, then quadrilateral formed by joining their end points is a
पर्याय
rhombus
rectangle
parallelogram
square
उत्तर
square
The given information in the form of the following figure is as follows:
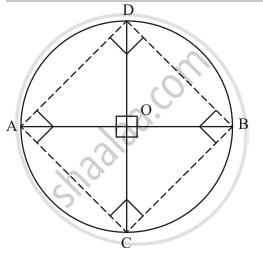
Since, four sides of the quadrilateral ACBD are four chords which subtend equal angles at the centre. Therefore,
`angleAOC = angleCOB = angleBOD = angleDOA = 90°`
(Since AB and CD are perpendicular diameters)
So sides AC, BC, BD and AD are equal, as equal chords subtend equal angle at the centre.
So , AC = CB = BD = DA …… (1)
We know that diameters subtend an angle of measure 90° on the circle.
So, `angle ACB = angleCBD = angleBDA = angleDAC = 90°` …… (2)
From (1) and (2) we can say that `square AC BD` is a square.
APPEARS IN
संबंधित प्रश्न
If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.
If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C, and D, prove that AB = CD (see given figure).

A circular park of radius 20m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk each other. Find the length of the string of each phone.
Find the length of a chord which is at a distance of 5 cm from the centre of a circle ofradius 10 cm.
Find the length of a chord which is at a distance of 4 cm from the centre of the circle of radius 6 cm.
Two chords AB and CD of a circle are each at distances 4 cm from the centre. Then AB = CD.
Two chords AB and AC of a circle with centre O are on the opposite sides of OA. Then ∠OAB = ∠OAC .
Two congruent circles with centres O and O′ intersect at two points A and B. Then ∠AOB = ∠AO′B.
AB and AC are two chords of a circle of radius r such that AB = 2AC. If p and q are the distances of AB and AC from the centre, prove that 4q2 = p2 + 3r2.
