Advertisements
Advertisements
प्रश्न
If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C, and D, prove that AB = CD (see given figure).

उत्तर
Let us draw a perpendicular OM on line AD.
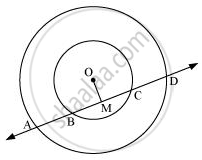
It can be observed that BC is the chord of the smaller circle and AD is the chord of the bigger circle.
We know that the perpendicular drawn from the centre of the circle bisects the chord.
∴ BM = MC ...(1)
And, AM = MD ...(2)
On subtracting equation (2) from (1), we obtain
AM − BM = MD − MC
⇒ AB = CD
APPEARS IN
संबंधित प्रश्न
If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
true or false
A circle has only finite number of equal chords.
Find the length of a chord which is at a distance of 5 cm from the centre of a circle ofradius 10 cm.
Two chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are opposite side of its center. If the distance between AB and CD is 6 cm. Find the radius of the circle.
If two diameters of a circle intersect each other at right angles, then quadrilateral formed by joining their end points is a
If AB is a chord of a circle, P and Q are the two points on the circle different from A and B, then
In a circle of radius 17 cm, two parallel chords are drawn on opposite side of a diameter. The distance between the chords is 23 cm. If the length of one chord is 16 cm, then the length of the other is
Two chords AB and CD of a circle are each at distances 4 cm from the centre. Then AB = CD.
Two chords AB and AC of a circle with centre O are on the opposite sides of OA. Then ∠OAB = ∠OAC .
Two equal chords AB and CD of a circle when produced intersect at a point P. Prove that PB = PD.
